¥ Title
and Authors
Simple
Mathematical Simulations for Event Driven Programming
Suranga
Hettiarachchi
Computer
Science Department
Indiana
University Southeast
New
Albany, IN 47150
¥ Objectives
Expose
students to event driven programming concepts using simple mathematical
simulations and introduce them to group projects in CS1/CS2 courses.
¥ Why
Is It Engaging
Modeling
and simulating mathematical problems are not very common in CS2 courses. The depth of the problems increases
student problem solving skills, technical communication skills, and
understanding of complex computational concepts. An interesting outcome is the
amount of discussions these problems generate.
¥ The
Exercise
There
are two examples, the first is simulating closest pair problem and the second
is simulating motion of a pendulum.
Students use graphical interfaces, event handlers, and timers to
implement software solutions to these problems. The mathematical basis of the
problems uses trigonometry, Pythagorean theory and periodic motion.
¥ Reasoning
Topics Covered
User interface design, event listeners, and trigonometry for
periodic motion, Pythagorean theory, brute force and/or recursive algorithms.
¥ Audience
First or second year undergraduates in CS1 and CS2
programming courses.
¥ Discussion
(Difficulty, Strengths, Weaknesses, Dependencies, Variants)
Instructor
can scale the difficulty of the first problem by introducing more
realistic physical aspects of pendulum motion (force laws) , and either using
brute force algorithm or a recursive algorithm can change the difficulty of the
closest pair problem.
Two
Examples: simulating closest pair
problem and the second is simulating motion of a
pendulum.
The first problem
is simulating closest pair
Design
of the simulated environment of Closest Pairs.
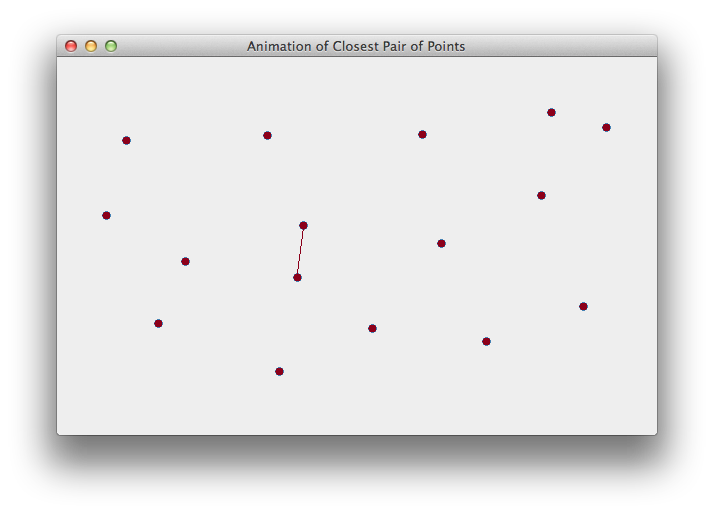
The
closest pair problem: There are two algorithms that can be used to solve this
problem
The straightforward problem is in
computational geometry though it has been applied to derive solutions to
different problems. The brute-force algorithm is O(N^2)
complexity. Of course there are much more efficient solutions to this problem
than this brute-force approach.
We need to know the minimum
distance between two points in a space with N points where each point is
defined by (x,y)
coordinates. We can exhaustively compute the distances between each pair (there
are N*(N-1)/2 pairs of points here) and pick the pair with the minimum
distance
minDistance <--- MaxInteger
ClosestPoint_p <--- unknown
ClosestPoint_q <---- unknown
for i
<---0 to N{
for j <-- 0 to N{
if ( (i
!= j) && distanceBetween(Point_i, Point_j) < minDistance){
minDistance <---- distanceBetween(Point_i, Point_j)
ClosestPoint_p
<--- Point_i
ClosestPoint_q
<---- Point_j
}
}
}
Closest
pair is defined by the points ClosestPoint_p
and ClosestPoint_q.
With
help of Pythagorean Theorem, we can find the distance
between two points.
If
the two points have following coordinates,
Point_i = (x_i, y_i)
Point_j = (x_j, y_j)
Distance
between the the two points can be found by
Square
root of ((x_j - x_i) 2 +
( y_j
- y_i)2)
We
can also use a recursive algorithm to solve this same problem. You may find that Vectors or ArrayLists are also suitable data structures.
may use a container like
function closest_pair(l,r) { // l- left most index, r - right most index
//P[l...r] ->array containing all the points
//assume
P[l...r] is sorted by
x-coordinate <----use Quicksort
O(nlogn)
if size(P)<2 // there should be at least two points to
process
return infinity;
mid=(l+r)/2; // middle index
midx=P[mid].x; //x-coordinate of
the middle index
//recursive
calls to the left of the midx and right of the midx
dl=closest_pair(l, mid); //
closest pair left of midx
dr=closest_pair(mid+1,
r); //closest pair right of midx
//side
effect: P[l...mid] and
P[mid+1...r] are sorted by y-coordinate (due to merge)
delta=min(dl, dr);//minimum
distance given from dl and dr
//QL
contains all the points delta distance left of midx
QL=select_candidates(l, mid, delta, midx);
//QR
contains all the points delta distance right of midx
QR=select_candidates(mid+1, r, delta, midx);
//dm is the closest pair in the 2*delta region from midx
dm=delta_m(QL,
QR, delta);
//
merge makes P[l..r] sorted by y-coordinate
merge(l, mid, r);
//
closest pair is the one with minimum distance of these
three
return min(dm, dl, dr);
}
select_candidate(l, r, delta, midx) {
//from P[l...r] select
all points which are in the distance at most delta from midx
line
create empty array Q
for(i=l to r) // for all the
points from left to right of this half
//
find the ones that lies less than delta distance from midx point
if(abs(P[i].x-midx)<=delta)
store P[i] in Q
return Q;
}
function delta_m(QL,
QR, delta) {
//are
there two points p in QL, q in QR such that d(p,q)<=delta?
//n is the number of data points
// QL and QR are sorted in ascending order by y-coordinates
j=1; dm=delta; //this is the
minimum we know so far
for(i=1 to size(QL)) for all the
points in the left
pt=QL[i];
// is there a
point in the right side in the interval y-delta
while(j<=n and QR[j].y<pt.y-delta)
j=j+1;
k=j;
//
check for all the points to the right in the interval y+delta
while(k<=n and QR[k].y<pt.y+delta)
//
store the minimum, if there is any such points
dm= min(dm,
dist(pt, QR[k]));
k=k+1;
return dm;// this is the minimum
found so far in the middle region
}
The second
problem is simulating motion of a pendulum.
Design
of the simulated environment of Pendulum.
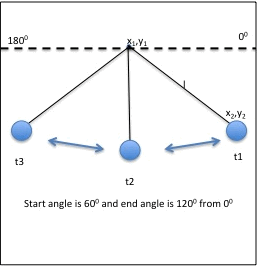
The t1, t2, and t3
are specific time steps. The pendulum
starts at time t1 at 60degree angle (right most angle) and once it reaches
120degrees (left most angle) at time t3, the pendulum swings the other way. The
letter l represents the length of the string/rod. We are not modeling this
pendulum swing using force laws, we can ignore all that for now, if someone is
interested in modeling the pendulum swing using forces, you are welcome to do
so.
The point (x1, y1) is fixed, and we need to
find the position of the bob (x2, y2) for every degree change in angle. We can check the angle as follows,
If (angle is less than the right most
angle)
increment angle_delta // want to swing left
else
decrement angle_delta //want to
swing right
update the angle by adding angle_delta
Now
we know the angle, we can use bit of trigonometry to find the position (x2,y2)
x2 = x1 + l cos(angle)
y2 = y1 + l sin(angle)
Angle
must be in radians not degrees.