Christopher J. Kimmer, Ph.D.
IU Southeast Informatics
iSci
the informatics of scientific computing
Constructing an inflation matrix
As an example, the inflation matrix for a particular choice of the sixteen possible rules based on the cosets of the vertices lifted to 6D will be constructed. This is possible for all of these inflation rules, but some choices of rules lead to much more tedious checking of specific cases than others. The rule considered here will consist of always locating the short 3- and 5-fold separations after inflation close to the original endpoints of the short sticks that were integral. This rule creates a primitive cubic icosahedral tiling since it only distinguishes between integral and body-centered coordinates.
Another consequence of the simplicity of this rule is that each tile
inflates in at most two distinct ways. It is clear that the two
half-pyramids which each contain only one small face will inflate in two
ways, LL and SS.
The situation is different for the tetrahedra, however, since each of
them possess two small faces that determine their inflation. The
tetrahedron
T
1
is determined by specifying the inflation of two small
faces that share a long 5-fold edge that lifts to
{100000}
so that the
two faces will inflate the same way with this integer-based inflation
rule. Thus, there is only one way to inflate
T
1
in this scheme and
it corresponds to the LLSS inflation listed above.
The tetrahedron
T
2
contains the two faces that share a short 5-fold
edge that lifts to points like
½
{1111
![]()
![]() }
. One
small face will have its short 3- and 5-fold edges inflated close to one
endpoint of the shared edge, and the other will have the edges inflated
far away. The only possible inflation is once again the LLSS one.
}
. One
small face will have its short 3- and 5-fold edges inflated close to one
endpoint of the shared edge, and the other will have the edges inflated
far away. The only possible inflation is once again the LLSS one.
To write down the inflation matrix, the only extra knowledge needed is how many of each tile is formed during inflation. There are 2 ways to inflate two tiles and 1 one way each for the other two tiles, so there are 6 distinct kinds of tiles; the inflation matrix will be 6 x 6 with rows and columns listed in the order T 1 , T 2 , O 1 SS, O 1 LL, O 2 SS, O 2 LL:
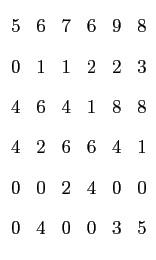 Z
≡
Z
≡
|
( 55 ) |
This matrix has, as expected, a largest eigenvalue of τ6 , and the right eigenvector for this eigenvalue yields relative frequencies of
|
( 56 ) |
and this eigenvector can be verified to obey the necessary ratio of the relative frequencies of T 2 and O 2 tiles
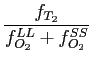 =
½
.
=
½
.
|
( 57 ) |
There is nothing particularly special about this inflation rule; it just happens to be the simplest to specify. In a similar manner, inflation matrices and tile frequencies can be worked out for the other 15 coset-based inflation rules.
Chris Kimmer 2011-06-01
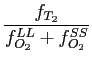 , 1),
, 1),