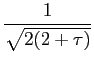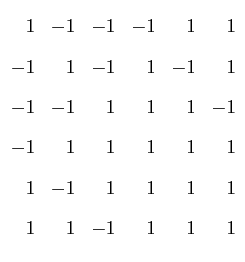Christopher J. Kimmer, Ph.D.

IU Southeast Informatics

iSci

the informatics of scientific computing

The Mathematics of Quasiperiodicity

In order to model a quasiperiodic minimal surface, the higher-dimensional formalism for quasicrystals described in Chapter 1 must be used. With this higher-dimensional approach, the tilings of Chapter 3 can be characterized by their acceptance domains decorating each higher-dimensional lattice point, and the tilings' construction by inflation rules can be outlined in detail. In this chapter, the higher-dimensional formalism not only allows a description of the minimal surface as the physical-space cut of the interface of a binary phase separation, but also allows the study of the critical surface in perp space, the 3D subspace orthogonal to the physical 3-plane.

The symmetry group of the icosahedron, Y _h , consists of rotations about two-fold, three-fold, and five-fold axes of symmetry in addition to the inversion operator. Y _h contains 120 elements, and the group may be factored into the 60 element icosahedral group Y containing pure rotations and the two-element group generated by inversion. Whenever the term ``icosahedral group'' or ``icosahedral symmetry'' is used, the full 120-element group Y _h is meant.

Icosahedra cannot be packed to fill space without leaving gaps, and in general, periodic structures with an icosahedrally-symmetric point group cannot be formed. Icosahedral symmetry is observed in materials with quasiperiodic ordering, and the diffraction patterns of these quasicrystals have Bragg peaks which can be indexed by six integers grouped into three pairs of golden integers of the form

n ₁ + n ₂ τ n ₁ , n ₂ ∈ $\displaystyle \mathbb {Z}$

( 2 )

where τ = ${\frac{{1 + \sqrt{5}}}{{2}}}$ is the golden mean. For arbitrary integral n ₁ and n ₂ , n ₁ + n ₂ τ densely and uniformly fill the real line, and a consequence of this filling is that there is no shortest distance between Bragg peaks (although the tremendous variation in peak intensity allows individual peaks to be resolved). In three dimensions, the set of numbers generated by the span of the six integers may also be obtained by the projection of the six dimensional hypercubic lattice $\displaystyle \mathbb {Z}$ ⁶ onto a totally irrationally-oriented, three-dimensional subspace, and this construction can form the basis for many quasiperiodic tilings.

Specifically, $\displaystyle \mathbb {Z}$ ⁶ may be decomposed into two orthogonal three dimensional subspaces denoted para (parallel) and perp (perpendicular), each of which contains a three dimensional irreducible representation of the icosahedral group. Axis conventions are those of Elser[ 27 ] where the projections of the six dimensional basis vectors $\hat{{e}}_{1}^{}$ = (100000) , etc. are of equal length in the two subspaces and together with their inverses point to the vertices of an icosahedron. The para subspace corresponds to physical space, while the orthogonal subspace is a conjugate representation with permutations of the 6D coordinate directions. Specifically, the rotation matrix from the 6D lattice basis ( n ₁ , n ₂ , n ₃ , n ₄ , n ₅ , n ₆ ) to the para and perp basis is

$\displaystyle \left(\vphantom{ \begin{array}{c} x_\parallel y_\parallel... ... z_\parallel x_\perp y_\perp z_\perp \end{array} }\right.$ $\displaystyle \begin{array}{c} x_\parallel y_\parallel z_\parallel x_\perp y_\perp z_\perp \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{c} x_\parallel y_\parallel... ... z_\parallel x_\perp y_\perp z_\perp \end{array} }\right)$ = $\displaystyle {\frac{{1}}{{\sqrt{2(2 + \tau)}}}}$ $\displaystyle \left(\vphantom{ \begin{array}{rrrrrr} \tau & 0 & 1 & 0 & 1 & ... ...1 & 0 & 1 & 0 & -\tau 0 & \tau & 1 & -\tau & 1 & 0 \end{array} }\right.$ $\displaystyle \begin{array}{rrrrrr} \tau & 0 & 1 & 0 & 1 & \tau -1 & \t... ... \tau & 1 & 0 & 1 & 0 & -\tau 0 & \tau & 1 & -\tau & 1 & 0 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{rrrrrr} \tau & 0 & 1 & 0 & 1 & ... ...1 & 0 & 1 & 0 & -\tau 0 & \tau & 1 & -\tau & 1 & 0 \end{array} }\right)$ $\displaystyle \left(\vphantom{ \begin{array}{c} n_1 n_2 n_3 n_4 n_5 n_6 \end{array} }\right.$ $\displaystyle \begin{array}{c} n_1 n_2 n_3 n_4 n_5 n_6 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{c} n_1 n_2 n_3 n_4 n_5 n_6 \end{array} }\right)$ .

( 3 )

Projection into para(perp) space is then implemented by the upper(lower) half of this matrix, and may be denoted as P _∥ ( P _⊥ ) .

Similar notions can be employed to construct quasilattices by projection from other lattices in six dimensions. Beyond the 6D simple cubic lattice, the only other two icosahedral lattices are the face-centered and body-centered hypercubic lattices[ 28 ] which may be defined in analogy with their 3D counterparts. The FCC lattice may be formed by taking the subset of the simple cubic lattice whose coordinates sum to an even number. The BCC lattice may be defined by considering two SC lattices translated by (½½½½½½) relative to each other. As in three dimensions, these lattices are dual to each other so that the diffraction pattern from a BCC lattice is FCC and vice versa.

Finally, icosahedral quasilattices are self-similar in that changes of scales in physical and perp space leave the projected 6D lattice invariant. In particular,

P _∥ (2 $\displaystyle \bar{{1}}$ $\displaystyle \bar{{1}}$ $\displaystyle \bar{{1}}$ 11) = τ ³ P _∥ (100000)

( 4 )

and

P _⊥ (2 $\displaystyle \bar{{1}}$ $\displaystyle \bar{{1}}$ $\displaystyle \bar{{1}}$ 11) = - τ ^-3 P _⊥ (100000)

( 5 )

illustrate a means to map the 6D SC lattice onto itself by transforming the basis vectors with these changes of scale. This transformation can be written as an operation on a 6D vector without regard to the two subspaces

M ³ (100000) = (2 $\displaystyle \bar{{1}}$ $\displaystyle \bar{{1}}$ $\displaystyle \bar{{1}}$ 11),

( 6 )

and the operation of M ³ is said to be an ``inflation by τ ³ ''. More generally, the action of M ⁿ in 6D is ``inflation by τ ^-3 '', which transforms the two subspaces by scaling the parallel space projection up by τ ⁿ and scaling the perp space projection down by - τ ^{-

n} . The inflation matrix M is

M ≡ ½ $\displaystyle \left(\vphantom{ \begin{array}{rrrrrr} 1 & -1 & -1 & -1 & 1 & ... ... 1 & -1 & 1 & 1 & 1 & 1 1 & 1 & -1 & 1 & 1 & 1 \end{array} }\right.$ $\displaystyle \begin{array}{rrrrrr} 1 & -1 & -1 & -1 & 1 & 1 -1 & 1 & -... ...& 1 & 1 1 & -1 & 1 & 1 & 1 & 1 1 & 1 & -1 & 1 & 1 & 1 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{rrrrrr} 1 & -1 & -1 & -1 & 1 & ... ... 1 & -1 & 1 & 1 & 1 & 1 1 & 1 & -1 & 1 & 1 & 1 \end{array} }\right)$

( 7 )

which maps the 6D FCC and BCC lattices onto themselves; they are invariant under inflations by τ . The inverse process of scaling down in para space and up in perp space is known as deflation, and the deflation matrix is given by M ^-1 = M - 1 . The behavior under inflation for the four cosets of points making up the BCC lattice is shown in Table 2.1 .

**Table 2.1:** The behavior of a point x under the action of M . The point x belong to a coset by having all integral or half-integral coordinates and then by the parity of its coordinates' sum.
Coset	M	M ²	M ³
Int, Even	Int, Even	Int, Even	Int, Even
Int, Odd	Half-Int, Even	Half-Int, Odd	Int, Odd
Half-Int, Even	Half-Int, Odd	Int, Odd	Half-Int, Even
Half-Int, Odd	Int, Odd	Half-Int, Even	Half-Int, Odd

Beyond the indexing of diffraction peaks, the same basic approach can be used to construct quasilattices as point sets obtained by projection from a higher-dimensional periodic lattice. Rather than projecting the entire 6D lattice into para or perp space, which densely covers para space, subsets can be obtained by projecting only the lattice points whose perp space projections lie in a given ``window,'' where the window is a three-dimensional object in perp space. An alternate yet equivalent method is to decorate each lattice point with a three-dimensional acceptance domain (AD) lying in perp space and form the quasilattice by cutting $\mathbb {R}$ ⁶ with a 3-plane x _⊥ = constant representing physical space. If the AD is chosen to be the inversion of the window used to projecting a vertex set, the projection and the cut will produce the same quasilattice. The generic intersection of the acceptance domain with physical space is a point, and the size and shape of the acceptance domain determines which quasilattice points lie in physical space for a given cut.

A quasilattice is then completely determined by the specification of a higher- dimensional lattice, the orientation of the two subspaces, and the form of the acceptance domains that decorate the lattice points. For the 6D to 3D icosahedral quasilattice construction, the quasilattice will have icosahedral symmetry if the AD is invariant under the action of the icosahedral group. Beyond quasilattices and point sets, icosahedrally symmetric quasiperiodic functions may be treated as the x _⊥ = constant cut of a periodic function in six dimensions by straightforward extensions of the above ideas, and it is this idea that makes this higher dimensional formalism attractive for the study of quasiperiodic minimal surfaces.

Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu

Valid XHTML | CSS