Christopher J. Kimmer, Ph.D.

IU Southeast Informatics

iSci

the informatics of scientific computing

Modelling a BPMS

Sheng and Elser used a Landau-Ginzburg free energy functional to model a minimal surface as an equilibrium interface between two phases. If an order parameter Ψ( x ) is used with Ψ( x ) = 1 for one phase and Ψ( x ) = - 1 for the other, the interface is given by the Ψ( x ) = 0 isosurface. Phase equilibrium corresponds to stationary solutions of the free-energy functional

F [Ψ( x )] = $\displaystyle \int$ κ|∇Ψ( x )| ² + (1 - Ψ( x ) ² ) ² d ⁿ x

( 8 )

in an n -dimensional space. The n - 1 dimensional Ψ = 0 hypersurface is a BPMS provided the group-subgroup symmetries discussed above are enforced. In the limit κ → 0 the energy is proportional to the area of the hypersurface and the Ψ( x ) = 0 isosurface is a minimal surface. This approach was initially studied in Reference [ 25 ] and nicely reproduces known periodic minimal surfaces as well as new ones in three dimensions, but it is unsuitable for representing an icosahedrally symmetric, quasiperiodic surface where there is no unit cell and the integration must be carried out over an infinite volume in 3D. In the six-dimensional representation of a quasiperiodic function, the integration over physical space becomes an integration over a single unit cell, and this obstacle is removed. The Ψ( x ) = 0 level set in 6D is a 5D hypersurface which leads to a 2D surface in physical space when cut by the 3-plane x _⊥ = constant. To ensure that the surface in physical space formed by the cut is minimal, a limiting procedure designed to treat the interface anisotropically with respect to the para and perp spaces must be used. The anisotropic functional can be expressed as

F [Ψ( x )] = $\displaystyle \int$ κ _∥ |∇ _∥ Ψ( x )| ² + κ _⊥ |∇ _⊥ Ψ( x )| ² + (1 - Ψ( x ) ² ) ² d ⁶ x

( 9 )

with ∇ _i denoting the projection of the gradient onto subspace i . To achieve the desired result of a minimal surface in physical space, one demands not only that κ _∥ and κ _⊥ go to zero but that

κ _⊥ /κ _∥ → 0

( 10 )

as well.

The evolution of Ψ( x ) as κ is reduced to zero may be followed numerically, but the simplest case, which is that of a planar interface, can be solved analytically. As the surface tension is reduced, the interface becomes sharper and approaches a kink or step-function. The order parameter is

Ψ( x ) = tanh(x κ ^-½ )

( 11 )

with a free energy of (8 κ) ^½ per unit interfacial area, corresponding to a transition region between Ψ( x ) = - 1 and Ψ( x ) = + 1 with a thickness ∼ κ ^½ . All the energy density is concentrated in the transition region.

The inequality of κ _∥ and κ _⊥ in Equation 2.8 is equivalent to a rescaling of the para and perp subspaces. The mapping

( x _∥ , x _⊥ ) → ( αx _∥ , α ^-1 x _⊥ ).

( 12 )

implies the gradients in each of the subspaces transform according to

κ ₀ (|∇ _∥ Ψ( x )| ² ,|∇ _⊥ Ψ( x )| ² ) → κ ₀ ( α ^-2 |∇ _∥ Ψ( x )| ² , α ² |∇ _⊥ Ψ( x )| ² ).

( 13 )

This transformation conserves 6-volume and maintains icosahedral symmetry, and α < 1 is a stretching of perp space relative to para space. Of course, the interface is not actually stretched, but the inequality of κ _∥ and κ _⊥ allow this interpretation. Making the association κ _∥ = κ ₀ / α ² and κ _⊥ = κ ₀ α ² indicates that the evolution t → 0 leads to stable solutions of Equation 2.8 that are stretched in perp space; the Ψ( x ) = 0 isosurface is the product of a 3-plane in perp space and a minimal surface in physical space. However, the translational symmetry of Z ⁶ implies that the interface's perp space structure cannot be globally planar; there will be kinks or steps. Consequently, the leading terms of the energy will be of the form

F ∼ $\displaystyle \sqrt{{8\kappa_\parallel}}$ A _∥ + $\displaystyle \sqrt{{8\kappa_\perp}}$ V _∥

( 14 )

where A _∥ is the area of the minimal surface in parallel space. The first term gives the contribution of the minimal surface in physical space to the energy, and the V _∥ term subsumes the energy cost associated with the envelope of the kinks in perp space.

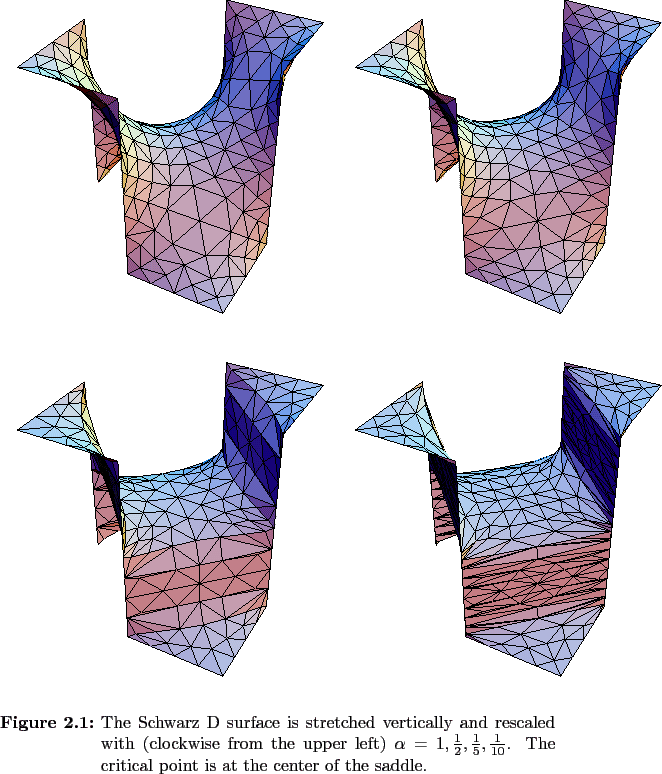
The interpretation discussed in the above paragraph can actually be implemented by changing the boundary conditions rather than modifying the gradient terms. Hoffman[ 30 ] pursued a similar idea in order to form new periodic minimal surfaces in 3D from existing ones by stretching the underlying lattice of the original minimal surface. With this approach, a surface with cubic symmetry stretched along a coordinate axis becomes a surface with tetragonal symmetry. If the 5D surface were to actually be constructed with this stretching technique, it would have to be rescaled after being stretched in order to satisy the original periodic boundary conditions of Z ⁶ . Also, the stretching would have to be in the three perp space dimensions and not just along one direction. Evolving an interface based on this idea is essentially a two-step process. First, the surface is stretched adiabatically to create a stable surface obeying the stretched boundary conditions, and then the surface is rescaled to the original boundary conditions. To implement the process numerically, α starts at the unstretched value of 1 and is lowered incrementally. Each time α is decremented, the energy of the new configuration is minimized.

A lower dimensional analogue of the generation of one minimal surface from a higher dimensional periodic one by stretching its lattice is easy to compute and visualize. For the Schwarz D surface (see Figure 2.1 ), a BPMS with the symmetry of a diamond lattice, the stretching direction can be taken to be along a coordinate axis, say the z direction, shown as vertical in the subsequent figures showing this process. Parallel space is then defined to be the x - y plane, and the goal is to obtain zero curvature ``surfaces'' (straight lines) in this plane by cutting the stretched surface with the plane z = constant. The evolution of the stretched and then rescaled D surface is shown in Figure 2.2 .

**Figure 2.1:** The Schwarz D surface
$\begin{figure} \begin{center} \leavevmode\epsfysize =3.in \epsffile{dcell2.eps} \end{center} \end{figure}$

$\begin{figure} % latex2html id marker 363 \begin{center} \leavevmode $ \beg... ... is at the center of the saddle.} \normalspacing \end{center} \end{figure}$

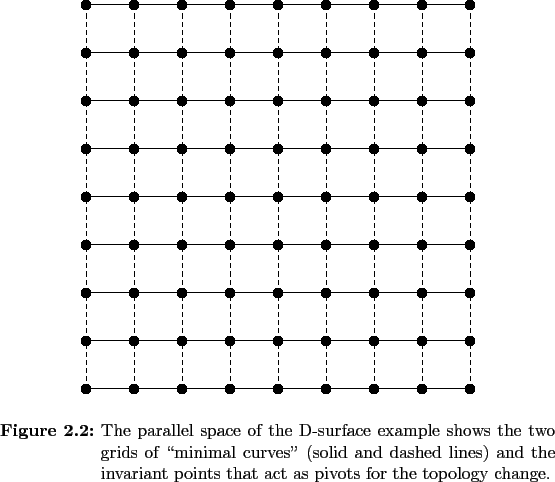
Stretching along the z direction creates a surface that is locally planar, and in the limit of infinite stretching followed by the rescaling, a cut by an x - y plane forms a set of parallel lines. Depending on the z -coordinate of the cut plane, these lines are oriented in one of two ways with the two orientations related by a rotation about the z -axis of 90 ^o . Stretching along the z -axis has broken the cubic symmetry, but the quotient group of the octahedral group consisting of symmetry operations that leave the z direction unchanged remain symmetry operations of the surface. There is a topology change or transition between the two families of lines in physical space as the z coordinate describing the cut plane is changed. The critical z -value for the topology change is the point where the surface normal is along the z direction (it lies entirely in the perp space), and as the cut plane passes through this point, the family of parallel lines cut by the plane changes orientation. Also of interest are the points that are symmetry related to this critical point on the unstretched surface. Their projections onto the x - y plane are independent of the choice of z coordinate for the cut, and the square lattice of points in physical space formed in this way is the scaffolding about which the topology change from one set of lines to another takes place (see Figure 2.3 ).

$\begin{figure} % latex2html id marker 382 \begin{center}\epsfxsize =3.5in ... ...pivots for the topology change. } \normalspacing \end{center} \end{figure}$

This geometric interpretation of the process whereby a stretched minimal surface may be cut to produce new minimal surfaces of lower symmetry in a lower dimensional space reveals that the method embodied in this process and in Equation 2.8 may be generalized to construct many new minimal surfaces with desired symmetry properties. In the 6D case studied here, the stretching along the perp directions breaks the hypercubic symmetry and leads to the icosahedrally symmetric structure.

Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu

Valid XHTML | CSS