iSci

the informatics of scientific computing

next up previous
Next: The Voronoi Construction at Up: Discrete Structure of the Previous: Discrete Structure of the

The Voronoi Construction

To consider the power and ease of construction of a cell complex that shares the same topology as a minimal surface, it is useful to examine the Schwarz P surface. Like the quasiperiodic minimal surface, it is defined on a BCC lattice where one labyrinth unites one simple cubic sublattice while the other labyrinth connects an SC sublattice translated by a body center. The surface is well-approximated by the zero surface

cos(2 π x ) + cos(2 π y ) + cos(2 π z ) = 0 ( 23 )

if a cubic lattice constant of 1 is assumed. The maxima of this function are the integral lattice points and the minima are the maxima translated by a body center. The positive labyrinth connects maxima directed along the coordinate axes, and of course, the negative labyrinth is the positive one translated by a body center.

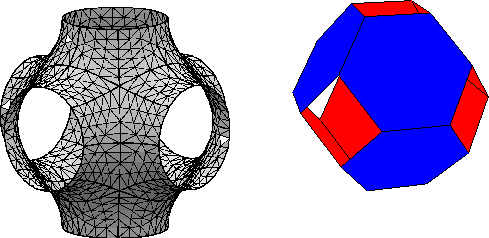
Since the extrema form a BCC lattice, a cell complex capturing the topology of the P surface can quickly be generated by considering the set of all points closer to one BCC lattice point than any other. This set of points is alternatively called the Voronoi cell, Wigner-Seitz cell, or Dirichlet domain, and the Voronoi cell complex is well-defined for any discrete point set. For the 3D BCC lattice, the Voronoi cell is a truncated octahedron, and each face is dual to a lattice vector. The hexagonal faces separate maxima from minima and correspond (very roughly) to the location of the interface. The square faces along the coordinate directions separate maxima from maxima or minima from minima, so they may be eliminated. The Voronoi construction is illustrated in Figure   2.9 .

Figure 2.9: The modified Voronoi cell of the BCC lattice creates a cell complex that has the same topology as the Schwarz P surface.
\begin{figure} \centering $\begin{array}{cc}\epsfxsize =2.0in \epsffile{p... ...le{truncoct.eps} \end{array}$ \singlespacing \normalspacing \end{figure}

This Voronoi construction for generating a cell complex with the same topology as a given minimal surface is generalizable and practical to implement whenever a simple analytic approximating function that can furnish extrema is available. It works well for many other balance periodic minimal surfaces in three dimensions, and in higher dimensions. The N-dimensional P surface is the minimal surface approximated by

Ψ ( x ) = $\displaystyle \sum_{i}^{}$ cos 2 π x i = 0 ( 24 )

which once again defines a balance minimal surface on a N-dimensional BCC lattice with maxima at integral points and minima at half integral points. In six dimensions, this is the isotropic surface formed by the Landau-Ginzburg free energy minimization for t = 1 before the three-fold amplitudes become large. The Voronoi construction carried out for the 3D P surface can be repeated in six dimensions using the discrete point set formed by the extrema of Ψ ( x ) . At t = 1 , Ψ ( x ) is the 6D P surface, and the extrema are the 6D BCC lattice points. As t → 0 , the extrema of Ψ ( x ) are no longer situated at lattice points, and a different cell complex approximating the surface in the limit of infinite stretch can be computed. For the Voronoi constructions at t = 1 or small t approximating t → 0 , faces of the 6D Voronoi cells are 5-dimensional and dual to two extrema of Ψ ( x ) . Faces dual to extrema of the same sign are deleted, and the result is a cell complex in six dimensions that captures the topology of the surface.

next up previous
Next: The Voronoi Construction at Up: Discrete Structure of the Previous: Discrete Structure of the
Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu