iSci

the informatics of scientific computing

next up previous
Next: A Set of Tiles Up: An Ensemble of Quasiperiodic Previous: An Ensemble of Quasiperiodic

Introduction

Quasiperiodic tilings are the dominant theoretical tool for the description of the atomic structure of quasicrystals. As alluded to earlier, they may be generated by substitution rules in physical space or used to decorate vertex sets created by irrational cuts through a higher-dimensional lattice decorated with acceptance domains lying in perp space. The two viewpoints are equivalent and complementary; the lattice points that produce a vertex set upon projection into physical space yield the acceptance domain of the vertices when projected into perp space. As discussed in Section 2.1, the icosahedral lattices in 6D contain four cosets of points which can be taken as coordinates that are all integral or half-integral with even or odd coordinate sums. For a tiling with vertices from more than one coset, the subset of vertices in physical space belonging to a single coset may be conjugated into perp space to determine an AD that decorates the 6D FCC lattice of that particular coset.

The symmetry of a vertex set can be classified based on which cosets have ADs at their lattice points and whether or not two or more cosets of points have identical ADs. For instance, a tiling with the same AD placed at lattice points belonging to all four cosets is body-centered icosahedral (BCI) whereas a tiling with all four cosets decorated by different ADs is face-centered icosahedral (FCI). A tiling with two pairs of distinct ADs is simple icosahedral (SCI). Of course, all cosets of lattice points do not have to have ADs. For instance, the 3DPT is formed by placing triacontahedra in perp space on the SC lattice defined by the integral coordinates. Likewise, the Danzer tiling[ 33 ] is an FCI tiling which has only three of the four cosets decorated[ 34 , 35 ].

All 3D quasiperiodic tilings in the literature with known ADs have polyhedral ADs, but a tiling can have a fractal or curved AD, as well. Many two dimensional tilings are known which have fractal acceptance domains, and in many of these tilings, there are related families of tilings with different ADs that have the same tiles, vertex densities, and other properties[ 36 , 37 , 38 , 39 , 40 ]. In all of these tilings, the inflation rules used to construct them may be varied to generate the family of tilings, but the combinatorical properties of the inflation rule are unchanged while the geometric arrangements of the tiles change. The vertex density is proportional to the volume of the AD[ 6 ], so related tilings with the same vertex density can also be characterized by families of ADs with the same volume and symmetry.

A concise way to represent many aspects of an inflation rule is by use of an inflation matrix which gives combinatorial information about the subdivision of each inflated tile into copies of the prototiles. To illustrate with the familiar square-triangle tiling[ 41 ], which is a two-dimensional tiling made up of squares and equilateral triangles with all edge lengths 1, the inflation matrix will be examined. A triangle can be scaled up by σ ≡ 2 + $ \sqrt{{3}}$ and decomposed into 7 triangles and 3 squares while a square can be scaled by σ and tiled by 16 triangles and 7 squares yielding the inflation matrix[ 41 ]

$\displaystyle \singlespacing$ $\displaystyle \cal {M}$ = $\displaystyle \left(\vphantom{ \begin{array}{cc} 7 & 16 3 & 7 \end{array} }\right.$ $\displaystyle \begin{array}{cc} 7 & 16 3 & 7 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{cc} 7 & 16 3 & 7 \end{array} }\right)$ . $\displaystyle \normalspacing$ ( 27 )

Multiplication on the left by a vector whose components are the areas of the triangle and square, respectively, represents the fact that the re-tiling by the prototiles fills the inflated volume of the original tile so 7 triangles plus 3 squares tile an area σ2 times the area of one triangle. The corresponding statement for the subdivision of the square holds true, too, and implies

( A $\scriptstyle \bigtriangleup$ , A $\scriptstyle \Box$ ) $\displaystyle \cal {M}$ = σ2 ( A $\scriptstyle \bigtriangleup$ , A $\scriptstyle \Box$ ). ( 28 )

In other words, σ2 is an eigenvalue of this matrix, and it is in fact the largest one. Multiplication by a vector on the right can be interpreted as the combinatorial action of an inflation rule where the components of the vector are the numer of triangles ( N $\scriptstyle \bigtriangleup$ ) squares ( N $\scriptstyle \Box$ ) in a patch of tiling that is to be enlarged by inflation

$\displaystyle \singlespacing$ $\displaystyle \cal {M}$ $\displaystyle \left(\vphantom{\begin{array}{c} N_\bigtriangleup N_\Box\end{array} }\right.$ $\displaystyle \begin{array}{c} N_\bigtriangleup N_\Box\end{array}$ $\displaystyle \left.\vphantom{\begin{array}{c} N_\bigtriangleup N_\Box\end{array} }\right)$ = $\displaystyle \left(\vphantom{\begin{array}{c}\tilde{N}_\bigtriangleup \tilde{N}_\Box\end{array}}\right.$ $\displaystyle \begin{array}{c}\tilde{N}_\bigtriangleup \tilde{N}_\Box\end{array}$ $\displaystyle \left.\vphantom{\begin{array}{c}\tilde{N}_\bigtriangleup \tilde{N}_\Box\end{array}}\right)$ $\displaystyle \normalspacing$ ( 29 )

yielding a larger tiling with $ \tilde{{N}}_{\bigtriangleup}^{}$ triangles and $ \tilde{{N}}_{\Box}^{}$ squares. Successive inflations correspond to repeated multiplication by $ \cal {M}$ , so that in the limit of infinite inflation, the product is dominated by the normalized eigenvector, ( e $\scriptstyle \bigtriangleup$ , e $\scriptstyle \Box$ ) , associated with the largest eigenvalue, σ2 :

$\displaystyle \singlespacing$ $\displaystyle \lim_{{n \rightarrow \infty}}^{}$ $\displaystyle \cal {M}$ n = σ2n $\displaystyle \left(\vphantom{ \begin{array}{r} e_\bigtriangleup e_\Box \end{array} }\right.$ $\displaystyle \begin{array}{r} e_\bigtriangleup e_\Box \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{r} e_\bigtriangleup e_\Box \end{array} }\right)$ . ( e $\scriptstyle \bigtriangleup$ , e $\scriptstyle \Box$ ). $\displaystyle \normalspacing$ ( 30 )

The relative frequencies of triangles and squares, f $\scriptstyle \bigtriangleup$ and f $\scriptstyle \Box$ , is then

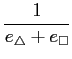
$\displaystyle \singlespacing$ $\displaystyle \left(\vphantom{ \begin{array}{r} f_\bigtriangleup f_\Box\end{array}}\right.$ $\displaystyle \begin{array}{r} f_\bigtriangleup f_\Box\end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{r} f_\bigtriangleup f_\Box\end{array}}\right)$ = $\displaystyle {\frac{{1}}{{e_\bigtriangleup + e_\Box}}}$ $\displaystyle \left(\vphantom{ \begin{array}{r} e_\bigtriangleup e_\Box \end{array} }\right.$ $\displaystyle \begin{array}{r} e_\bigtriangleup e_\Box \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{r} e_\bigtriangleup e_\Box \end{array} }\right)$ . $\displaystyle \normalspacing$ ( 31 )

For any square-triangle tiling formed by inflation rules, there are $ {\frac{{4}}{{\sqrt{3}}}}$ triangles for every square which implies that half the area of the tiling is filled by squares and the other half by triangles.

It is possible to construct square-triangle tilings by a variety of inflation rules resulting in different ADs, which all behave topologically the same way as the cut is moved in perp space. When the cut leaves one AD, it immediately enters two others that share a common boundary with the AD just left. That there is not a one-to-one correspondence between the boundary elements of one AD and the boundaries of other ADs is a way of stating that the square-triangle tilings do not obey the gluing condition[ 42 ]. The gluing condition is a means of ensuring that vertices (or more physically, atoms in a structure model) do not appear or disappear as the cut plane is moved in perp space; vertices simply undergo bounded phason jumps as the cut plane leaves one AD and enters another that is glued to the first one. The 3DPT tiling affords an example of a tiling that satisfies the gluing condition, for the centroids of the faces of the triacontahedral AD of the 3DPT bisect the projection of a two-fold lattice vector into perp space. The faces are mirror planes of symmetry and are shared by two ADs displaced relative to each other by the two-fold lattice vector, satisfying the gluing condition.

Kalugin studied the constraints the gluing condition places on densities in a quasicrystal by assuming that a given quasilattice's AD was glued one-to-one to other ADs[ 43 , 44 , 45 ]. He showed that in the case of icosahedral symmetry the density will necessarily be of the form

&rho0 ( N 1 + N 2 τ ),   N 1 , N 2 ∈ $\displaystyle \mathbb {Z}$ , ( 32 )

where the prefactor ρ0 depends upon the symmetry of the lattice and is also proportional to the magnitude cubed of a canonical diffraction wavevector for the lattice.

next up previous
Next: A Set of Tiles Up: An Ensemble of Quasiperiodic Previous: An Ensemble of Quasiperiodic
Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu