iSci

the informatics of scientific computing

next up previous
Next: Generating the tilings Up: An Ensemble of Quasiperiodic Previous: Introduction

A Set of Tiles Related to the Minimal Surface

Three-dimensional quasiperiodic tilings are of interest in this work since the topology jumps seen in the quasiperiodic minimal surface as the cut plane is moved in perp space are analagous to phason jumps in atomic quasicrystals and tile rearrangements in a tiling. The notion that these jumps are confined to a vanishingly thin region of perp space in the limit of infinite stretch of the 5D surface strongly hints at the relationship between the surface and quasiperiodic tilings.

The results of Chapter 2 indicate that the labyrinth structure of the quasiperiodic minimal surface is well-approximated by constructing a cell complex from the Voronoi cells of the extrema of the function $ \tilde{{\Psi}}$ ( x ) whose zero level set approximates the 5D surface. The 32 extrema closest to the origin having the same sign of $ \tilde{{\Psi}}$ ( x ) are grouped into 12 extrema along 5-fold directions and 20 along 3-fold directions; every 6D BCC lattice has 32 such extrema associated with it. Deleting the Voronoi faces shared by extrema of the same sign yields a discrete approximation with the same topology as the 5D surface, and this construction can shed light on what kind of edges or vertex separations a tiling corresponding to the minimal surface should have.

By studying the packing of the minimal-surface motifs in physical space (described in Section 2.7) with local icosahedral symmetry and labyrinths issuing forth along 5-fold directions, Elser conjectured that a tiling corresponding to the critical surface or the Voronoi construction of the quasiperiodic surface of Chapter 2 should have edges projected from the 5-fold 6D separations {100000} and ½ {11 $ \bar{{1}}$ 11 $ \bar{{1}}$ } and the 3-fold separations ½ { $ \bar{{1}}$ $ \bar{{1}}$ $ \bar{{1}}$ 111} and ½ {111111} [ 46 ]. Elser's intuitive construction can be strengthened by observing that by considering how to construct a tiling related to the minimal surface. In order to relate the physical-space surface to a tiling, a 6D BCC lattice point is projected into physical space if one of its associated extrema's Voronoi cells intersects the 3-plane x ⊥ = constant defining physical space. If two projected lattice points have associated extrema sharing a 5-face of the Voronoi construction's cell complex, a tiling constructed from the physical-space surface can reasonably be thought to have an edge connecting the two lattice points. In 6D, all the extrema sharing 5-faces in the Voronoi construction are associated with lattice points along an edge of the Deloné triangulation of the 6D BCC lattice, so a reasonable set of edges for a tiling constructed from the physical-space surface should be the entire set or a subset of these Deloné edges projected into physical space.

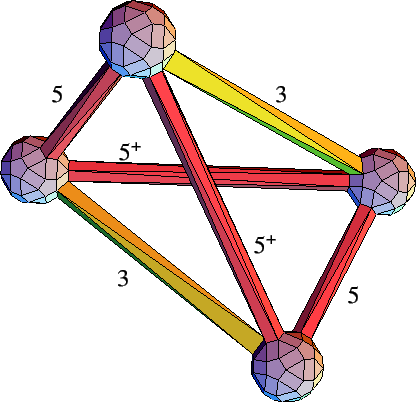
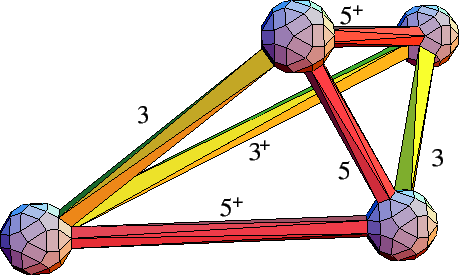
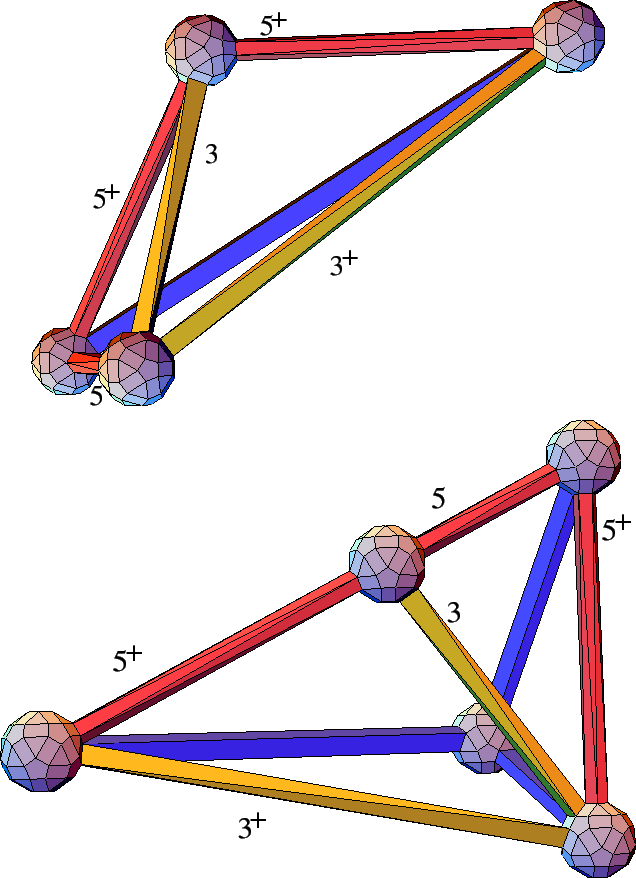
A tiling with a subset of the Deloné edges can be constructed by a set of four tiles consisting of two tetrahedra (Figures  3.1 and 3.2 ) and two half-pyramids (Figure  3.3 ). Although it has not been rigorously demonstrated that the tilings described below contain the tiling that should be associated with the minimal surface, in Chapter 4 the utility of this tiling for describing the local topology and geometry of the physical-space minimal surface will be made clear. The tiles as shown contain edges along three-, five-, and two-fold directions, but the half pyramids are always matched with themselves around the two-fold directions to yield a global tiling containing only edges along three- and five-fold directions. In particular, up to symmetry there are two three-fold edges with lengths of 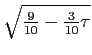$ \tilde{{3}}$ ≡ $ \sqrt{{\frac{9}{10}-\frac{3}{10}\tau}}$ = 0.644... and τ $ \tilde{{3}}$ and two five-fold edges with lengths $ \tilde{{5}}$ ≡ $ {\frac{{1}}{{2 \tau}}}$ = 0.437... and τ $ \tilde{{5}}$ . The vertices of a representative member of each type of tile are given in Table  3.1 .

Figure 3.1: The tetrahedron T 1 . Short 3- and 5-fold edges are labelled ``3'' and ``5'', respectively. Long 5-fold edges are labelled `` 5 + ''.
\begin{figure} \begin{center} \leavevmode\epsfysize =3.5in \epsffile{abbstile1.eps} \singlespacing \normalspacing \end{center} \end{figure}
Figure 3.2: The tetrahedron T 2 . Short 3- and 5-fold edges are labelled ``3'' and ``5'', respectively. Long 5-fold and 3-fold edges are labelled `` 5 + '' and `` 3 + '', respectively.
\begin{figure} \begin{center} \leavevmode\epsfxsize =4.in \epsffile{abbstile3.eps} \singlespacing \normalspacing \end{center} \end{figure}
Figure 3.3: The half-pyramids O 1 (top) and O 2 . Short 3- and 5-fold edges are labelled ``3'' and ``5'', respectively. Long 3-fold and 5-fold edges are labelled `` 3 + '' and `` 5 + '', respectively. Unlabelled edges are 2-fold edges.
\begin{figure} \begin{center} \leavevmode $\begin{array}{c}\epsfxsize =5.i... ...s} \end{array}$ \singlespacing \normalspacing \end{center} \end{figure}



Table 3.1: The vertices of the tiles: The vertex on the long 5-fold edge of the O 2 tile is not given.
T 1 (0, 0, 0) (1, 1 - τ , 0) ( τ , 1, 0) (1, 1, 1)
T 2 (0, 0, 0) ( τ , 1, 0) (1, 1, 1) (1, 1 + τ , 0)
O 1 (0, 0, 0) ( τ , 1, 0) ( τ , τ , τ ) ( τ , 1 + τ , 1)
O 2 (0, 0, 0) (1 + τ , τ , 0) ( τ , τ , τ ) ( ½ (1 + τ ), ½ + τ , ½ τ )

The two tetrahedra are labelled T 1 (Figure  3.1 ) and T 2 (Figure  3.2 ) with T 1 representing the tetrahedron with the least volume. The volumes of T 1 and T 2 are ⅓ and τ/3 , respectively. The other two tiles are labelled O 1 and O 2 (Figure  3.3 ) in order of increasing volume and in deference to the fact that 4 O 1 s or 8 O 2 s form octahedra. O 1 and O 2 are half-pyramids with volumes of τ/3 and $ {\frac{{1}}{{6}}}$ + τ/3 , respectively.

As evidenced in Figure  3.3 , the largest half-pyramid contains an extra vertex along the long five-fold edge. This vertex makes the tiling face-to-face in the sense that a single O 2 tile's face containing the 3-fold edge lying in it may match up 1-to-1 with another O 2 tile, or it may match up with two different tiles that share the edge lying in the face. This subdivision is perhaps inelegant, but it is completely equivalent to the alternative of subdividing O 2 into two tiles partitioned by the 3-fold edge in the face. This would introduce another tile to keep track of, and would be uninteresting since the two new tiles would always be glued together. Simplicity trumps face-to-face elegance.

next up previous
Next: Generating the tilings Up: An Ensemble of Quasiperiodic Previous: Introduction
Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu