iSci

the informatics of scientific computing

next up previous
Next: Pruning Vertex Sets Up: An Ensemble of Quasiperiodic Previous: A Set of Tiles

Generating the tilings

Although tilings with the four prototiles described in Section 3.2 arose in tandem with the study of the physical-space minimal surface of Chapter 2, it is far from trivial to directly relate a tiling to a minimal surface since the physical-space surface's topology is not completely known. As described in Section 2.7, regions of physical space associated with a lattice point whose projection into perp space is close to the origin (well inside the inner surface of the critical surface of Section 2.5) are unambiguously determined by the Voronoi construction and $ \tilde{{\Psi}}$ ( x ) . At lattice points whose perp-space projections are further from the origin, the details of the physical-space surface are less well-resolved, and it is not clear what topology the physical space surface has. Consequently, having an independent means to construct tilings as candidate scaffoldings for the minimal surface is desirable, and the construction of such tilings will be outlined here.

Inflation rules for the tiles can be defined where each tile is scaled in size by τ2 , additional vertices are added on the boundary of this larger volume, and the volume is re-tiled by the original four prototiles. Depending on which vertices are added after the τ2 inflation (the addition of these vertices is treated in detail below), there are 5 distinct ways to tile the τ2 -inflated T 1 , and 4 ways to re-tile the τ2 -inflations of the other tiles. For each tile, the τ2 inflations can be re-tiled in at least two combinatorially distinct ways; that is, the numbers of each type of tile used to re-tile an inflated volume depends on the additional vertices added by the inflation rule. Table  3.2 lists each possible combinatorial way to re-tile a given tile, and more detailed information about the particular inflations of each tile is given in Appendix A.



Table 3.2: The combinatorial properties of τ2 inflations of the tiles.
  T 1 T 2 O 1 O 2 Ways to tile
τ2 T 1 3 2 2 4 1
  4 1 5 2 3
  5 0 8 0 1
τ2 T 2 5 2 5 6 2
  6 1 8 4 2
τ2 O 1 6 2 7 4 3
  7 1 10 2 1
τ2 O 2 8 3 9 5 3
  9 2 12 3 1

The flexibility in subdividing an inflated tile opens the door for considerable freedom in creating tilings, but the addition of vertices along the boundaries of the τ2 -inflated tiles constrains the inflations of tiles that share faces or edges in a tiling. Consequently, the specification of the inflations of edges and faces can in turn specify how a tile containing that edge or face is inflated. The inflation of 2-fold edges, long 5-fold edges, and long 3-fold edges is uniquely defined. To specify the inflation of these edges, consider that tilings containing the two tetrahedra and two half-pyramids have both long and short edges along 2-, 3-, and 5-fold directions. Without regard to the symmetry of the edge being inflated, denote a long edge as L and a short edge (which is L's τ -deflation) as S. The inflation rule for a long edge is two successive applications of the Fibonacci substitution rule L → LS and S → L:

L → LSL. ( 33 )

A short 2-fold edge also unambiguously inflates to a single edge τ2 the original length, and this long edge is only found in an octahedron formed by the half-pyramids. There is ambiguity in the inflation of short 5-fold and 3-fold edges that create the different ways of inflating a tiling. For a given orientation of a short 5- or 3- edge S, either the rule S → LS or S → SL can be used; rather than specifying which way a tile inflates, it suffices to specify which of the two ways all short 3- or 5-fold edges inflate.

Alternatively, this process can be carried out as a vertex-based subsitution rule by defining an operation, $ \cal {G}$ , that ``grows'' a vertex set by augmenting a single vertex with 20 + 12 vertices that are translations of the original vertex along long 3- and 5-fold edges (see Figure  3.4 ). The $ \cal {G}$ operation may be defined over a set of vertices in order for successive applications of $ \cal {G}$ to be defined. Inflate (by τ2 ) the set of vertices and take the union of the inflated set plus the 32 translates of the set itself

$\displaystyle \cal {G}$ * { v i } = $\displaystyle \bigcup_{i}^{}$ { $\displaystyle \cal {G}$ * ( $\displaystyle \cal {I}$ v i )} ( 34 )

where $ \cal {I}$ inflates a point by τ2 if the point is a physical space point and by - τ-2 if the point is in perp space. In perp space, $ \cal {G}$ can be infinitely applied to a starting vertex to produce a dense point set that is the AD of the point set in para space after infinite application of $ \cal {G}$ ; this AD is believed to be a three-dimensional fractal object.
Figure 3.4: $ \cal {G}$ replaces the central vertex by 12+20 copies of itself in parallel space (top) and perp space. The short 3-fold edges introduced by application of $ \cal {G}$ to the central vertex are shown.
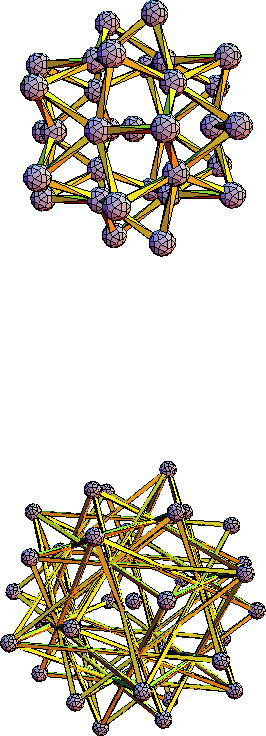
\begin{figure} \begin{center} \leavevmode $\begin{array}{c}\epsfysize =4.i... ...} \end{array} $ \singlespacing \normalspacing \end{center} \end{figure}

A recipe for building a tiling using $ \cal {G}$ can now be outlined. Beginning with a single vertex, (at the origin x 0 in physical space, say), an application of $ \cal {G}$ produces the 12+20 star of points in addition to leaving x 0 unchanged, but $ \cal {G}$ introduces short 3-fold separations as shown in Figure  3.4 . The next application of $ \cal {G}$ to the resulting vertex set creates too-short 3-fold separations between vertices that are incompatible with the edge lengths of the four tiles, so some of these vertices must be eliminated before there will be any hope of tiling the vertex set. The operation of ``tiling the vertex set'' identifies a correspondence between a vertex set and a tiling containing the four types of tiles if the union of the vertices in the tiling is the same as the vertex set itself. Tiling the vertex set will be denoted as $ \cal {T}$ , and $ \cal {T}$ is properly defined only when the vertex set is infinite and the tiling tiles all of space. The tiling of the vertex sets studied here is well-defined in that there are no vertex configurations that can be tiled in more than one way. It is also useful to speak of a finite vertex set as being ``tiled'' whenever the entire vertex set or some subset of it is the same as the union of the vertices of a finite tiled region of space.

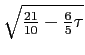In order to produce a vertex set with vertex separations consistent with the edges of the tiling, a pruning operation, $ \cal {P}$ , can be defined that removes the minimal number of vertices to eliminate the forbidden separations. After two applications of $ \cal {G}$ , all the shortest separations consist of pairs of vertices separated by a distance of $ {\frac{{\tilde{3}}}{{\tau}}}$ = $ \sqrt{{\frac{21}{10}-\frac{6}{5}\tau}}$ , which is a τ -deflation of the short 3-fold edge in the tiling. If icosahedral symmetry is to be preserved, there is only one choice to be made; the rest of the pairwise eliminations are determined by symmetry. $ \cal {P}$ is only completely specified, then, if there is some scheme to determine which vertices are to be deleted.

To summarize, a seed set can be created by starting with one vertex and applying $ \cal {G}$ twice followed by $ \cal {P}$ . This is a rather pedantic approach to generate a starting set, but now a tiling can be specified by

$\displaystyle \cal {T}$ * $\displaystyle \left(\vphantom{\prod_i ({\cal P}_i \ast {\cal G})}\right.$ $\displaystyle \prod_{i}^{}$ ( $\displaystyle \cal {P}$ i * $\displaystyle \cal {G}$ ) $\displaystyle \left.\vphantom{\prod_i ({\cal P}_i \ast {\cal G})}\right)$ * ( $\displaystyle \cal {G}$ 2 * x 0 ); ( 35 )

it is understood that the multiplication denoted above is like function composition--i.e. the order of operations is important. Growth ( $ \cal {G}$ ) followed by pruning ( $ \cal {P}$ ) can create larger and larger subsets of vertices that can be tiled, and in Equation  3.9 the notation $ \cal {P}$ i is used to parameterize the operator $ \cal {P}$ at each stage i . There is considerable freedom in choosing $ \cal {P}$ i , a specific rule may be adopted at each stage i , or a specific choice can be made for each pair of vertices (up to symmetry) in the stage.


Subsections
next up previous
Next: Pruning Vertex Sets Up: An Ensemble of Quasiperiodic Previous: A Set of Tiles
Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu