Christopher J. Kimmer, Ph.D.

IU Southeast Informatics

iSci

the informatics of scientific computing

Clusters of Too-close Vertices

The method for constructing a tiling by Equation 3.9 worked only because every operation of $\cal {G}$ (except the first two) was followed by $\cal {P}$ . If $\cal {P}$ is omitted, no points are ever eliminated and the fractal AD alluded to in Section 3.3 is constructed. The growth of a vertex set without pruning can be written as

$\displaystyle \cal {S}$ ≡ $\displaystyle \left(\vphantom{\prod_i {\cal G}}\right.$ $\displaystyle \prod_{i}^{}$ $\displaystyle \cal {G}$ $\displaystyle \left.\vphantom{\prod_i {\cal G}}\right)$ * ( $\displaystyle \cal {G}$ ² * x ₀ ). ( 36 )

The too-short edges that are never prumed in $\cal {S}$ are clearly incompatible with the edge lengths of the tiles, so $\cal {T}$ * $\cal {S}$ is ill-defined. It is clear that every vertex in $\cal {S}$ belongs to an infinite number of tilings formed by some appropriate choice of inflation rules; $\cal {S}$ is the superset of the ensemble of tilings formed by all the possible choices of inflation rules.

As $\cal {G}$ is successively applied to a starting vertex x ₀ , the action of $\cal {G}$ continues to introduces too-short separations along 3- and 5-fold directions. The AD of this tiling is bounded, so it is clear that there will still be a shortest separation between points in the tiling, and in fact, no shorter separations than the too-short 3- or 5-fold edges are introduced by omitting $\cal {P}$ . The local environments of vertices that are separated from other vertices by too-short separations can be divided into a few categories. The simplest configuration is when two vertices are joined by a single too-short edge, either along a 5-fold or 3-fold direction. Also appearing are groups of three vertices where one vertex is joined simultaneously to two others along too-short edges, either two 3-fold edges or one 3- and one 5-fold edge. Finally, there are groups of four vertices with a pair of too-short edges. In one case, one vertex is joined along both too-short 5- and 3-fold directions to two other vertices; in another case, a vertex is joined along two different too-short 3-fold edges (Figure 3.5 ). Finally, there are groups of four vertices joined by two too-short 3-fold edges and one too-short 5-fold edge (Figure 3.6 ).

**Figure 3.5:** A configuration of too-close vertices arising when the pruning operation is omitted. Yellow edges represent too-short 3-fold separations, and the red edge is a too-short 5-fold edge.
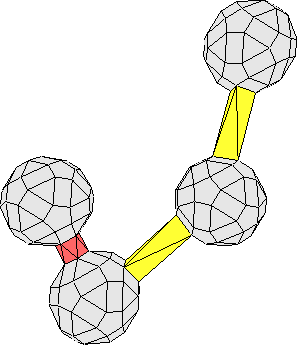
$\begin{figure} \begin{center} \leavevmode\epsfysize =3.in \epsffile{acolors.eps} \singlespacing \normalspacing \end{center} \end{figure}$

**Figure 3.6:** A second configuration (Figure 3.5 shows the first) of too-close vertices arising when the pruning operation is omitted. Yellow edges represent too-short 3-fold separations, and red edges are 5-fold.
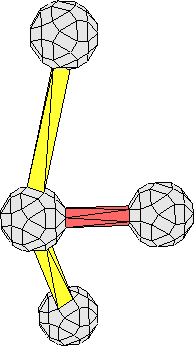
$\begin{figure} \begin{center} \leavevmode\epsfysize =3.in \epsffile{acolors2.eps} \singlespacing \normalspacing \end{center} \end{figure}$

In order to return to a tiling by the original tiles, more than a simple pruning operation where members of pairs are deleted is necessary since the configurations of too-close vertices are sometimes more complicated than simple pairs. For the triplets of vertices, either the one vertex with two too-short edges must be chosen, or the other vertices must be kept. Each of the two quadruplets of vertices must be treated differently.

The configuration shown in Figure 3.5 results from the application of $\cal {G}$ to a starting patch that is congruent to the τ -deflation of the large tile face containing long and short 3-fold edges, and this configuration arises whenever a too-short 3-fold edge has not been pruned. There are four possible ways reduce this configuration to one that $\cal {T}$ will be able to tile. Keeping a vertex with two too-short edges will uniquely determine the configuration while keeping a vertex with only one too-short edges forces a choice to be made between the two remaining vertices. All four of these choices lead to vertex configurations that arise in tilings constructed by inflation rules.

The quartet of vertices shown in Figure 3.6 arises from the application of $\cal {T}$ to the preceding paragraph's configuration. Examination of Figure 3.6 shows that the only free choice to be made in order to eliminate too-short separations occurs along the short 5-fold edge.

Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu

Valid XHTML | CSS