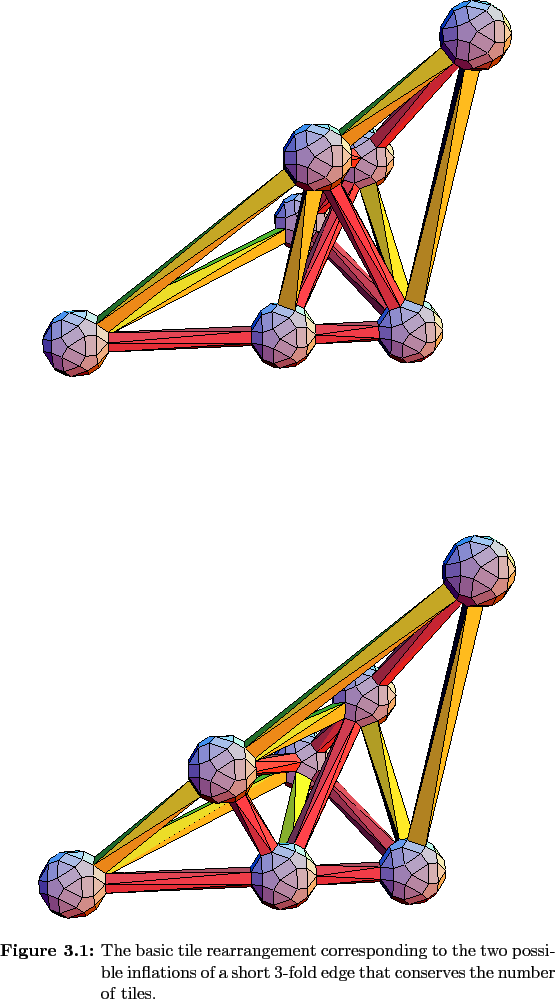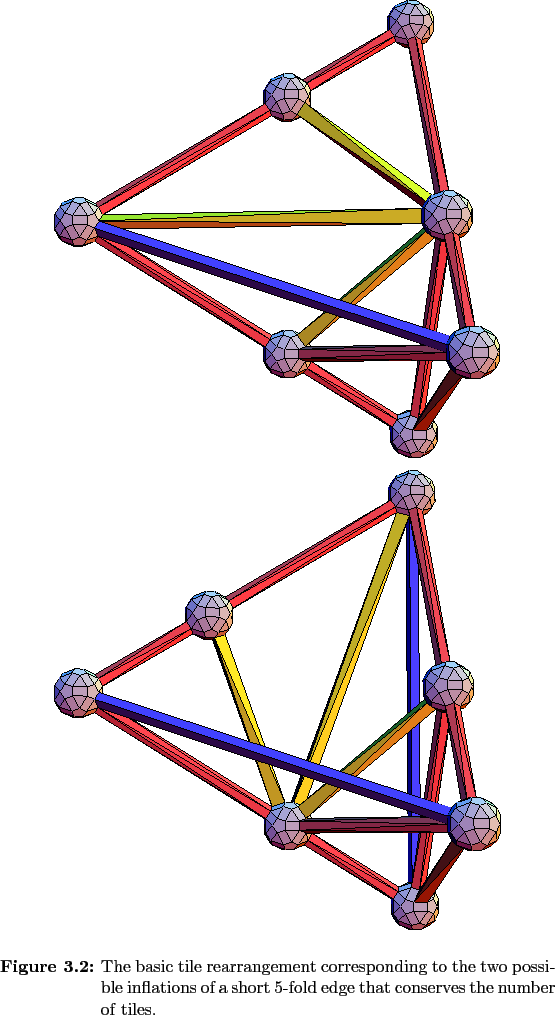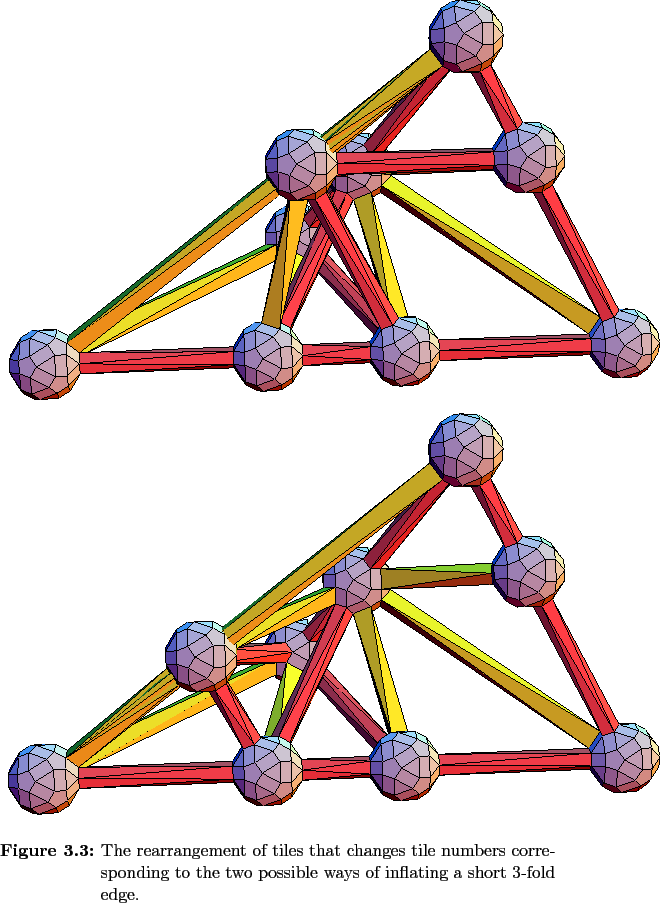Christopher J. Kimmer, Ph.D.
IU Southeast Informatics
iSci
the informatics of scientific computing
Next: Algebraic Structure of the Up: An Ensemble of Quasiperiodic Previous: Clusters of Too-close Vertices
Tile Rearrangements
The above discussion of inflation followed by pruning is completely equivalent to a tile-based inflation scheme, but since a given prototile may be re-tiled after inflation in different ways depending on its vertices, the nature of the inflation rules that can easily construct tilings is more obscured in tile-based inflation schemes. With the vertex-based scheme having been used to classify the possible inflation rules, it is now useful to examine the differences in the τ2 inflations of a given tile. Table 3.2 lists the distinct combinatorial ways to inflate a tile, and each tile has some inflations that are combinatorially equivalent, but not geometrically equivalent. The tile rearrangements between combinatorially-equivalent tile inflations conserve the numbers of each type of tile while combinatorially distinct inflations involve changes in tile number.
The variations in the inflation rules arise from the inflations of short 3- and 5-fold edges, and since all short edges in any tiling constructed with these rules belong to at least one small face that contains both a short 3-fold and a short 5-fold edge, the inflation of a tile can be reduced to the inflation of the small faces. A detailed treatment of the tile inflations arising from this conclusion is given in Appendix A. Here, the treatment will be more cursory and geometrically oriented. The choice of vertices along a short edge inherent in the inflation rules means that vertices will undergo phason jumps along these short edges. The tile rearrangments accompanying a vertex on a short edge undergoing such a phason jump are different depending on whether the jump occurs along a 3- or 5-fold edge.
There is one basic rearrangment along each symmetry direction that does not change the number of each kind of tile present. The rearrangement corresponding to a phason jump along a 3-fold edge is confined to a volume that is congruent to the T 2 tetrahedron scaled by τ , and it is tiled by 2 T 1 s, 1 T 2 , and 2 O 2 s. The rearrangement is related to the two-fold symmetry plane of the T 2 tile and consists of reflecting the tiles through this plane. This basic rearrangement is shown in Figure 3.7 , and it corresponds to a vertex jumping a too-short 3-fold distance.
Along a 5-fold direction, the basic tile-conserving rearrangment is not confined to a convex volume like the above 3-fold flip. The phason jump along the 5-fold edge is only tile-conserving when the 3-fold edge of the same short face has been inflated in such a way that the edge has been subdivided so that the long 3-fold edge has an endpoint in common with the 5-fold edge. The basic rearrangement here corresponds to 3 of the half pyramids, 1 O 1 and 2 O 2 s, rearranging themselves as shown (Figure 3.8 ) to accomodate the vertex that has moved.
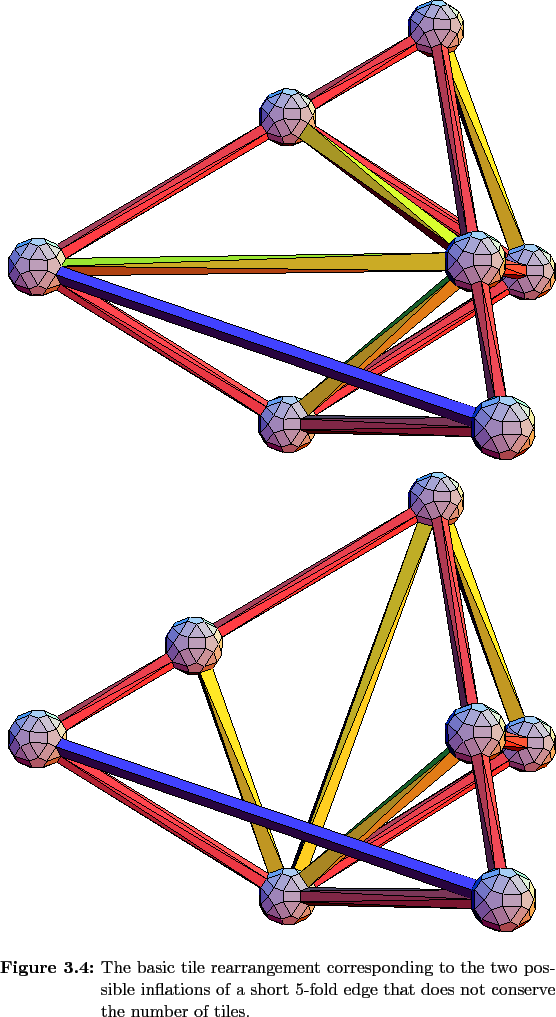
There is also a single type of tile rearangement along each symmetry direction that does not conserve the numbers of each type of tile, and these rearrangements are not confined to a convex volume like the tile-conserving jump along a 3-fold edge. Rearrangements caused by vertex-jumps along both symmetry directions consists of the disappearance(appearance) of a T 2 and 2 O 2 s followed by the appearance(disappearance) of a T 1 and 3 O 1 s. They correspond to a change in an entry in Table 3.2 of (1, - 1, 3, - 2) . The jump along a 3-fold direction that does not conserve tile numbers is shown in Figure 3.9 while Figure 3.10 shows the jump along a 5-fold edge.
Next: Algebraic Structure of the Up: An Ensemble of Quasiperiodic Previous: Clusters of Too-close Vertices