Christopher J. Kimmer, Ph.D.
IU Southeast Informatics
iSci
the informatics of scientific computing
The Existence of Minimal Surface Patches in the Tiles
Determining the minimal surface patch for the triangulated surface patches in each of the four tiles of Chapter 3 is a free-boundary problem since each tile face has a portion of the surface patch's boundary that is confined to that particular face yet free to move on the tile face. In Section 4.6, larger surface patches formed by matching up individual tile's triangulated patches across tile faces will be studied in order to study the the quasiperiodic minimal surface of Chapter 2 in large volumes in physical space. Here, a mathematical digression will be taken to study the existence of minimal surface patches with boundaries constrained to lie on a single tile's faces, and in Section 4.5, these surface patches in single tiles will be studied numerically.
It has been proven that any simple closed curve acting as a fixed
boundary supports a minimal surface[
23
],
but no such proof guarantees the equivalent solution for the free
boundary problem. One way to attack the problem is outlined in Reference
[
55
] and is based on the work of Hyde who showed that the existence
of solutions to the free-boundary problem on simplices could sometimes be
proven[
56
] based on the concept that every minimal
surface has an adjoint surface[
23
]; the adjoint transformation
(also called a Bonnet rotation of
90
o
)
is an isometric mapping taking every point
r
with normal vector
on a minimal surface
S
to a point
r'
on
S
's adjoint surface,
S'
, which is also
minimal. The surface normal
at
r'
is
; the adjoint transformation preserves the normal
vector. Finally, the tangent spaces at
r
and
r'
are related by
a
90
o
rotation about the normal vector,
. By means of such a
transformation,
surface patch contours constrained to lie on bounding planes
are mapped into straight lines while the normal vector is unchanged,
allowing the fixed boundary of the adjoint surface
S'
to be constructed
based only on the orientation of the free-boundary facets.
If the number and orientation of the boundary facets are such that
each portion of the fixed-boundary of
S'
can be closed
to form a polygon, the free-boundary problem on
S
has been
converted to a fixed boundary problem on
S'
. The fixed-boundary problem
will have a minimal solution, and the corresponding
free-boundary problem will, too.
In more detail, the bounding polygon of the adjoint surface depends on
S
's bounding volume's normal
vectors and the dihedral angles at each bounding facet's edge.
At a bounding face,
the surface meets the face plane at a right angle, and the normal vector
lies in the bounding plane. At a bounding edge,
S
lies in the corner
formed by two bounding planes, and the corresponding region of
S'
is a junction of two fixed edges defining the same angle as
the dihedral angle between the bounding planes meeting at
the bounding edge.
Finally, the rotation of the tangent space about
under
the adjoint transformation implies that the image of a free boundary
of
S
is a fixed boundary of
S'
that is
a straight line whose direction
is given by the normal direction of the original bounding plane;
free boundaries have been mapped to fixed straight lines.
To construct the fixed boundary of an adjoint surface, label the points on edges common to two boundaries of S as { v i } and number them so that v i and v i+1 share a common face. Label the edge each v i lies on as e i . The boundary of S' can be constructed by starting at v' 1 , which is the image of v 1 under the adjoint transformation. At v 1 , the normal vector is parallel to e 1 and defines a plane containing the fixed boundary of S' corresponding to the face containing e 1 and e 2 . A line from v 1 ' can be drawn an arbitrary distance in this plane along the direction given by e 1 x e 2 ; this line is an edge of the bounding polygon of S' , and two of its vertices, v 1 ' and v 2 ' are now defined. Proceeding from the point where the fixed-boundary line stopped, a new edge along the direction e 2 x e 3 can be drawn. Successive fixed-boundary directions, one for each contour of S constrained to lie on a bounding facet, can be determined by the cross products of consecutive edge vectors of the bounding facets. Now that all the edge directions of the fixed boundary have been specified, the edge lengths must be adjusted to close the polygon, if possible.
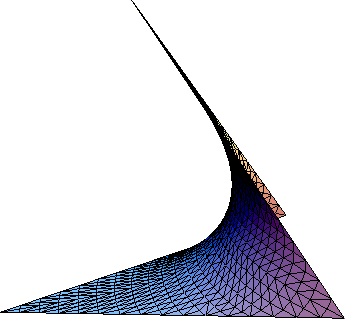
The construction of the bounding polygon is well-defined up to a scale factor (the segment lengths are arbitrary in the preceding construction) for a tetrahedral bounding surface provided the surface has only one contour along each face. If there is more than one boundary curve on a face, the construction must be handled case-by-case. In general for N boundary curves, there are N-4 degrees of freedom in the problem[ 56 ]. Consequently, of the four prototiles of Chapter 3, only the tetrahedron T 1 is immediately guaranteed to support a minimal surface wiht the same topology as obtained by carrying out the Voronoi construction using the extrema associated with each of its vertices. The adjoint surface patch for T 1 is shown in Figure 4.1 .
The next most simple tile to handle is the tetrahedron T 2 , but the adjoint construction is complicated by the fact that each of the large faces has two surface contours on it. The boundary polygon of the adjoint surface will have parallel edges on it, and in the parlance of the minimal surface community, this is known as the period problem[ 55 ]. For T 2 , the conditions imposed by the adjoint construction have no solution. The adjoint surface is then not embedded[ 55 ], so this method cannot be used to prove the existence of a minimal surface patch satisfying the boundary conditions. Applying the adjoint method to the two half-pyramids similarly leads to no solution, and numerical studies are the only available tools to characterize their curvature properties.
Chris Kimmer 2011-06-01