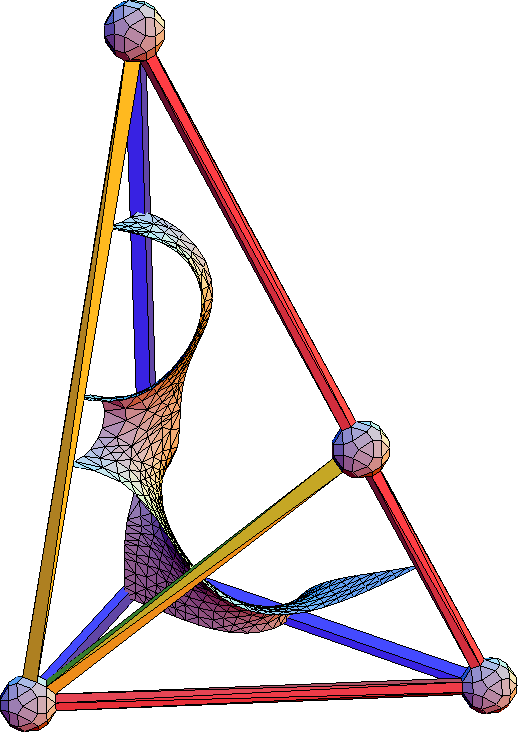iSci

the informatics of scientific computing

next up previous
Next: Larger Surfaces Up: Minimal Surface Approximations Previous: The Existence of Minimal

Numerical Results

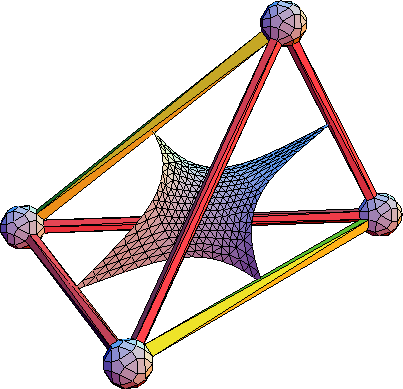
The evolution of the T 1 surface patch is interesting to follow since the existence of a minimal solution is guaranteed. When evolving the surface associated with the entire tile, the integral of squared mean curvature does not get as small as in the cases of other simple surface patches in tetrahedra associated with the periodic minimal surfaces. One problem is that the three two-fold planes in the T 1 tetrahedron frustrate the evolution. In general, if one jiggles the triangulation to escape a local minimum, the symmetry is broken, the effective number of degrees of freedom increases and the quality of the minimization compromised. A more numerically effective way to minimize this surface patch is to work with only 1/4 of it at a time by noting that the two fold planes imply that two straight lines lie in the surface. The straight lines lying in the surface act as a fixed boundary, and there is then only one free boundary left for Evolver to minimize. The number of degrees of freedom in the numerical evolution are reduced, and the numerical curvature properties are better. The results of the relaxation of the surface patch in the tetrahedron T 1 are shown in Table  4.4 . These results can be taken as a measuring stick of the quality of Evolver results, for since the minimal surface patch is known to exist, the data illustrate the behavior of the triangulation. The complete surface patch is shown in Figure  4.2 .

Figure 4.2: The relaxed T 1 surface patch
\begin{figure} \begin{center} \leavevmode\epsfxsize =3.5in \epsffile{bt1patch.eps} \end{center} \end{figure}



Table 4.4: Numerical data for the relaxation of the T 1 surface patch. These data are actually for one fourth of the surface.
Refinement A $ \int$ H 2 dA V E F θmax l max < ≅ >
1 .1545 2.96e-16 6 9 4 1.194 .659 0.0
2 .1369 1.13e-14 15 30 16 .471 .497 2.3e-8
3 .1359 2.44e-14 45 108 64 .242 .360 4.6e-8
4 .1357 2.23e-11 153 408 256 .128 .280 1.2e-7
5 .1357 3.60e-7 561 1584 1024 .071 .173 1.2e-5
6 .1357 9.42e-7 2145 6240 4096 .036 .091 2.2e-4
7 .1357 5.48e-8 8385 2476 16384 .018 .045 1.8e-2
8 .1357 2.64e-6 33153 98688 65536 .013 .022 2.4e-1




Table 4.5: Numerical data for the relaxation of the T 2 surface patch. These data are actually for one half of the surface.
Refinement A $ \int$ H 2 dA V E F θmax l max < ≅ >
1 .4597 3.28e-7 36 82 47 .594 .306 6.6e-7
2 .4561 4.15e-7 118 305 188 .335 .208 1.1e-7
3 .4553 4.78e-8 423 1174 752 .177 .104 2.0e-7
4 .4551 1.68e-9 1597 4604 3008 .096 .068 2.1e-4
5 .4551 2.62e-8 6201 18232 12032 .070 .031 6.0e-4
6 .4551 6.21e-7 24433 72560 48178 .043 .016 1.6e-4




Table 4.6: Numerical data for the relaxation of the O 1 surface patch.
Refinement A $ \int$ H 2 dA V E F θmax l max < ≅ >
1 .9513 3.46e-3 158 411 254 1.206 .275 3.7e-3
2 .9442 4.68e-3 503 1394 1892 .898 .180 5.5e-3
3 .9417 6.32e-3 1864 5368 3505 .442 .100 6.8e-3
4 .9411 6.65e-3 7232 21251 14020 .299 .051 6.4e-3
5 .9410 6.81e-3 28483 84562 56080 .167 .026 6.5e-3




Table 4.7: Numerical data for the relaxation of the O 2 surface patch
Refinement A $ \int$ H 2 dA V E F θmax l max < ≅ >
1 1.2735 3.31e-4 96 236 141 1.244 .373 1.58e-3
2 1.2425 5.09e-3 276 728 453 .728 .182 5.04e-3
3 1.2381 4.11e-3 919 2569 1651 .679 .112 4.12e-3
4 1.2365 4.03e-3 3485 10082 6598 .456 .067 4.22e-3
5 1.2361 4.17e-3 13567 39958 26392 .244 .033 6.44e-3

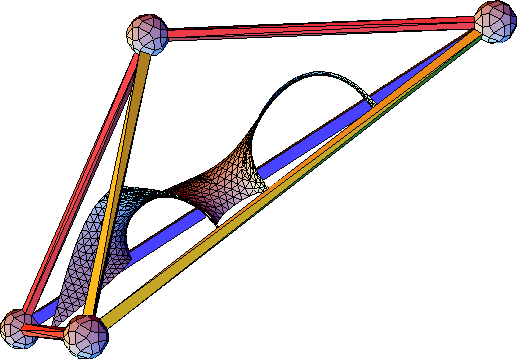
Like the T 1 surface patch relaxation, the relaxation of T 2 's surface patch is best-achieved by taking advantage of symmetry and not relaxing the full surface patch. The two-fold plane of T 2 implies that the surface patch contains a fixed straight line which may be used as a fixed boundary to improve the quality of the numerical results. These results are shown in Table  4.5 , and the full surface patch is shown in Figure  4.3 . This patch is highly stable with respect to its refinements as the energy is practically invariant with respect to the number of triangles. This is a good sign that the triangulation is close to a almost-minimal surface, but no more definitive statement can be made.

Figure 4.3: The relaxed T 2 surface patch
\begin{figure} \begin{center} \leavevmode\epsfxsize =4.in \epsffile{bt3patch.eps} \end{center} \end{figure}

The two half-pyramids cannot be dissected further by symmetry, so the full surface patches must be relaxed. Consequently, their curvature properties are not as good as those of the tetrahedra. Numerical results are given in Tables  4.6 and  4.7 while the surface patches are shown in Figures  4.4 and  4.5 . The discrete Willmore energies shown are much worse than the corresponding values for the tetrahedra's surface patches. One observation worth making is that the integral of squared mean curvature for O 1 and O 2 is highly triangulation-dependent. Some triangulations can be relaxed to an energy that is several orders of magnitude less than the ones shown, but they fail the other tests necessary to ensure a good triangulation. In general, the longest edge lengths will barely decrease from refinement to refinement and the maximum dihedral angle will not go to zero. The evolution of these triangulated surface patches will tend to from both very large (relative to the average triangle area) and very elongated (relative to the average edge length) triangles along the high-curvature boundary curves of the two half-pyramids, and the large changes in the normal vector's direction along the boundary curves are suspect. These surface patch instabilities can only be alleviated by starting with a much finer triangulation. The finer mesh has the consequence of increasing the degrees of freedom so that minimization takes a substantially longer time. Since the Landau-Ginzburg studies of Chapter 2 offer no hints that the quasiperiodic surface does not exist, it is felt that these problems reside in the algorithm used to approximate and minimize the surface rather than in the geometry of the surface patches themselves.

Figure 4.4: The relaxed O 1 surface patch
\begin{figure} \begin{center} \leavevmode\epsfxsize =4.5in \epsffile{t2patch.eps} \end{center} \end{figure}
Figure 4.5: The relaxed O 2 surface patch
\begin{figure} \begin{center} \leavevmode\epsfxsize =4.5in \epsffile{bt4patch.eps} \end{center} \end{figure}

next up previous
Next: Larger Surfaces Up: Minimal Surface Approximations Previous: The Existence of Minimal
Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu