Christopher J. Kimmer, Ph.D.
IU Southeast Informatics
iSci
the informatics of scientific computing
Larger Surfaces
The problems with evolution by mean curvature inherent in the surface patches of O 1 and O 2 are magnified when larger regions of space are tiled and larger triangulated surfaces are formed by matching surface patches across tile faces. The energy given by the integral of squared discrete mean curvature should roughly be additive as larger triangulated surfaces are constructed using more than one tile's surface patch. Since the curvature properties of larger triangulations will be at best as good as those of the O 1 and O 2 tiles' surface patches, it can be considered a small victory if larger surfaces do no worse than would be predicted by adding the energies of the individual tiles' surface patches together. Also, since the area converges well over several refinements even when the numerical curvature properties are poor, the use of the Surface Evolver is a good way to compute the area of triangulated surfaces in successively larger volumes. The simplest triangulations used for each tiles' surface patch affords a way to compute the genus per unit volume of these surface patches.
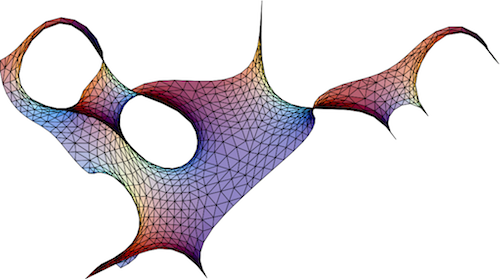
In order to gain reasonable estimates for the area and genus per unit volume of the quasiperiodic surface studied in Chapter 2, larger surfaces formed by matching individual tile's surface patches across tile faces in one fundamental region of icosahedral symmetry will be examined. The surface in this region will be truncated by a pseudo-mirror plane normal to the two-fold axis of the chosen fundamental region. Consequently, each bounded surface studied will be in a region congruent (up to a scale factor) to the O 2 tile or, equivalently, to 1/120 of a triacontahedron. Three successive inflations of the pseudo-mirror planes will be considered, and the first corresponds to the O 2 tile and its surface patch that has already been studied (Figure 4.6 ). The τ -inflation of this volume is tiled by 6 tiles and will also be studied. Finally, the τ2 -inflation of the O 2 tile with its surface patch will be evolved.
The tiling from Chapter 3 has a core of 7 tiles (in one fundamental domain--840 tiles overall) near the origin that is independent of the choice of inflation rules, and 6 of these tiles tile a volume that is congruent to the O 2 tile inflated by τ . The bounded surface associated with these tiles corresponds to the observed topology of the minimal surface near the origin in physical space, so this surface will provide an estimate of the area and genus per unit volume of the surface. The relaxed surface is shown in Figures 4.7 and 4.8 and the geometrical properties are listed in Table 4.8 .
At the next largest inflation scale, there are 4 τ2 inflations of the O 2 tile and 4 associated bounded surfaces that can partition space out to this distance (Appendix A gives details of the tile inflations). In the terminology of Appendix A, the SS inflation of O 2 corresponds to the observed topology of the quasiperiodic minimal surface in physical space. The curvature properties of the larger surfaces such as this one, and indeed of the core of 6 tiles examined earlier, are similar to the O1 and O2 tiles' properties, and they are relatively constant over successive refinements of the triangulation. Numerical data are given in Table 4.9.
![\includegraphics*[1.25in 1in][7in 7.25in]{t4orbit.eps}](t4orbit.png)
|
|
| Refinement | A |
|
V | E | F | θmax | l max | < ≅ > |
| 1 | 5.2190 | 7.35e-3 | 211 | 537 | 324 | 1.178 | .423 | 1.4e-2 |
| 2 | 5.1386 | 8.77e-3 | 748 | 2044 | 1294 | .705 | .266 | 3.45e-2 |
| 3 | 5.1195 | 1.13e-2 | 2773 | 7915 | 5140 | .379 | .134 | 6.33e-2 |
| 4 | 5.1149 | 1.31e-2 | 10688 | 31250 | 20560 | .201 | .067 | 1.4e-2 |
| 5 | 5.1138 | 1.37e-2 | 41597 | 123169 | 81570 | .114 | .033 | 5.21e-2 |
| Refinement | A |
|
V | E | F | θmax | l max | < ≅ > |
| 1 | 22.141 | 4.27e-1 | 720 | 1980 | 1243 | 1.170 | .541 | 1.5e-2 |
| 2 | 21.776 | 6.26e-1 | 2699 | 7686 | 4970 | .619 | .280 | 1.9e-2 |
| 3 | 21.690 | 7.17e-1 | 10380 | 30267 | 19870 | .336 | .140 | 2.1e-2 |
| 4 | 21.668 | 7.48e-1 | 40647 | 120144 | 79480 | .182 | .070 | 2.1e-2 |

|
For these three successive truncations by pseudo-mirror planes, the genus of each bounded surface can be calculated by summing the genera of the individual surface patches belonging to the individual tiles in the volume. The genus of a bounded surface is obtained from the Euler characteristic, which for a triangulation with N v vertices, N e edges, and N f faces is
| χ = N v - N e + N f . | ( 53 ) |
The Euler characteristic is a topological invariant, so it is independent of the specific triangulation used for a given topology. Each patch in a single tile has the topology of a disk and consequently an Euler characteristic of 1, but since tiles' triangulations share edges and vertices, this sharing must be taken into account. A triangle edge on a tile face is really only half an edge since it would otherwise be double counted, and likewise for triangle vertices on tile faces. Triangle vertices on tile edges count as 2 π divided by the dihedral angle at that edge. The genus g is simply related to χ by
| g = - χ / 2. | ( 54 ) |
The genus per unit volume is often used to characterize
periodic minimal surfaces that otherwise have infinite genus[
57
],
and the Euler characteristic and genus for each tile's surface patch is
given in Table
4.10
.
| Tile | χ/2 | g |
| T 1 | -7/15 | 7/30 |
| T 2 | -13/15 | 13/30 |
| O 1 | -37/30 | 37/60 |
| O 2 | -7/5 | 7/10 |
Given knowledge of the areas and genera of the bounded surfaces, the
genus per unit volume can be calculated.
Table
4.11
shows these values. To compare, Sheng found an area per unit
volume of
1.12
and a genus per unit volume of
.257
using the 5/3
rational approximant[
25
].
| Bounding Region | Volume | Genus/Volume | Area/Volume |
| O 2 | 1/6 + ⅓ τ | .254 | 1.11 |
| Core of 6 tiles | τ3 ( 1/6 + ⅓ τ ) | .256 | 1.09 |
| Inflated O 2 | τ6 ( 1/6 + ⅓ τ ) | .249 | 1.08 |
Chris Kimmer 2011-06-01