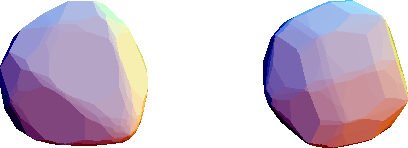Christopher J. Kimmer, Ph.D.
IU Southeast Informatics
iSci
the informatics of scientific computing
The t → 0 Voronoi Construction
Since Equation
2.14
gives an isosurface that well approximates the
minimal surface and is presumed to have the same topology as the limit
structure,
a natural way to obtain a cell complex for the limit surface is to
attempt the Voronoi construction
outlined above. A quick stab at the Voronoi cells of the extrema of
![]() (
x
)
reveals
that this cell complex does
not capture the topology of the surface, so a closer examination is
merited. The extrema of
(
x
)
reveals
that this cell complex does
not capture the topology of the surface, so a closer examination is
merited. The extrema of
![]() (
x
)
closest to the
origin are
{
¼
,
¼
, 0,
(
x
)
closest to the
origin are
{
¼
,
¼
, 0,
![]() ,
,
![]() ,
¼
}
and
{
¼
,
¼
,
¼
, 0, 0, 0}
along
five- and three-fold directions, respectively. The extrema here have
,
¼
}
and
{
¼
,
¼
,
¼
, 0, 0, 0}
along
five- and three-fold directions, respectively. The extrema here have
![]() = 6
, which differs in sign from
= 6
, which differs in sign from
![]() (000000) = - 4
.
(000000) = - 4
.
The inflation symmetry of the icosahedral quasilattice provides a means to change the relative scales of parallel and perp space, and consequently, the topology of the cell complex in 6D formed by a Voronoi construction depends on the scale used. If the real space coordinates are deflated by τ according to
|
x
= (
x
||
,
x
⊥
)
→
(
|
( 25 ) |
the order parameter field is invariant if the Fourier modes are inflated by τ
|
k
= (
k
||
,
k
⊥
)
→
(
τ
k
||
, -
|
( 26 ) |
The new dominant stars of wavevectors corresponding to Equation 2.14 are ½ {1
The extrema of
![]() (
x
)
can be deflated to give
the extrema of
(
x
)
can be deflated to give
the extrema of
![]() (
x
)
, and
in this process the closest lattice point to each extremum changes. The
maxima
along 5-fold directions are now closest to
{100000}
lattice points, so they may be translated by these lattice vectors to
obtain the
minima
closest to the origin
(
x
)
, and
in this process the closest lattice point to each extremum changes. The
maxima
along 5-fold directions are now closest to
{100000}
lattice points, so they may be translated by these lattice vectors to
obtain the
minima
closest to the origin
![]() {11
{11
![]()
![]()
![]() 1}
. The situation is slightly
different for the maxima along 3-fold directions. The maxima are of the form
1}
. The situation is slightly
different for the maxima along 3-fold directions. The maxima are of the form
![]() {
{
![]()
![]()
![]() 111}
which are equidistant from the
origin and a 3-fold lattice point
½
{
111}
which are equidistant from the
origin and a 3-fold lattice point
½
{
![]()
![]()
![]() 111}
.
In order to associate 12
+
20 maxima or minima with the closest lattice point
with the same sign of
111}
.
In order to associate 12
+
20 maxima or minima with the closest lattice point
with the same sign of
![]() , the 3-fold maxima can be translated
to obtain the minima
, the 3-fold maxima can be translated
to obtain the minima
![]() {
{
![]()
![]()
![]() 333}
. By associating these translated
minima with the origin, the Voronoi construction can be repeated with the
new inflation conventions, and the topology formed by this cell complex
agrees with the topology of the
333}
. By associating these translated
minima with the origin, the Voronoi construction can be repeated with the
new inflation conventions, and the topology formed by this cell complex
agrees with the topology of the
![]() (
x
) = 0
surface.
At the FCC grid points used in the
n
= 32
calculation, the sign of
Ψ
(
x
)
agrees with the sign predicted by the Voronoi construction at
96% of the points.
Figure
2.11
illustrates the agreement between the real-space
data and the Voronoi construction.
(
x
) = 0
surface.
At the FCC grid points used in the
n
= 32
calculation, the sign of
Ψ
(
x
)
agrees with the sign predicted by the Voronoi construction at
96% of the points.
Figure
2.11
illustrates the agreement between the real-space
data and the Voronoi construction.
Once the appropriate inflation scale is identified,
the Voronoi cells and Deloné triangulation can be calculated.
These calculations were carried out using the free software
qhull[
32
].
About each 6D BCC lattice point, there are 32 associated extrema of
![]() (
x
)
(but only 2 symmetry-inequivalent extrema),
and each extremum's Voronoi cell
contains the central lattice point as part of its boundary.
Surrounding this lattice point
is a motif consisting of the bounding faces of the Voronoi cells.
Interestingly, the Voronoi cells of these extrema along five- and three-
fold directions have the same volume, which by symmetry is 1/64. Moreover,
these two symmetry-inequivalent Voronoi cells are in fact
related by a symmetry
operation that interchanges parallel and perp space. A single
extremum's Voronoi cell, as calculated by qhull, contains 202 5-faces,
142 of
which separate
extrema of different sign and belong to the cell complex describing
the topology of the isosurface. As a rule, the Deloné edges dual to
these faces are not along high symmetry directions, but there are
exceptions. Extrema associated with the same lattice point share 5-faces
that are not part of the discrete approximation to the
Ψ
= 0
surface,
and a subset of these faces
have normal vectors (a.k.a. Deloné edge directions) along 2-fold
directions. For the 5-faces associated with Voronoi faces belonging to
the cell complex, there are 2 5-faces with normal vectors along 5-fold
directions. Their normal vectors are related by inversion, and these two
faces turn out to have particular importance. A Voronoi cell has
5 other 5-faces in the cell complex with Deloné edges along two-fold
directions; these faces will be important, too. The projection of the Voronoi
cell of an extremum into parallel and perp spaces is shown in
Figure
2.6.3
.
(
x
)
(but only 2 symmetry-inequivalent extrema),
and each extremum's Voronoi cell
contains the central lattice point as part of its boundary.
Surrounding this lattice point
is a motif consisting of the bounding faces of the Voronoi cells.
Interestingly, the Voronoi cells of these extrema along five- and three-
fold directions have the same volume, which by symmetry is 1/64. Moreover,
these two symmetry-inequivalent Voronoi cells are in fact
related by a symmetry
operation that interchanges parallel and perp space. A single
extremum's Voronoi cell, as calculated by qhull, contains 202 5-faces,
142 of
which separate
extrema of different sign and belong to the cell complex describing
the topology of the isosurface. As a rule, the Deloné edges dual to
these faces are not along high symmetry directions, but there are
exceptions. Extrema associated with the same lattice point share 5-faces
that are not part of the discrete approximation to the
Ψ
= 0
surface,
and a subset of these faces
have normal vectors (a.k.a. Deloné edge directions) along 2-fold
directions. For the 5-faces associated with Voronoi faces belonging to
the cell complex, there are 2 5-faces with normal vectors along 5-fold
directions. Their normal vectors are related by inversion, and these two
faces turn out to have particular importance. A Voronoi cell has
5 other 5-faces in the cell complex with Deloné edges along two-fold
directions; these faces will be important, too. The projection of the Voronoi
cell of an extremum into parallel and perp spaces is shown in
Figure
2.6.3
.
It is worth an aside to note that the Voronoi cells computed by qhull are computed using floating point arithmetic. This is much faster than using arbitrary precision arithmetic, but it has its price. Voronoi 5-faces are not planar to arbitrary precision and consequently bound a 6-dimensional volume. This imprecision makes it difficult to determine whether or not the face's normal vector is along a high-symmetry direction, so 5-face normal vectors are best-computed using the Deloné triangulation rather than the 5-faces of the Voronoi cells obtained from qhull.
Chris Kimmer 2011-06-01