iSci

the informatics of scientific computing

next up previous
Next: Core and Variable Vertices Up: An Ensemble of Quasiperiodic Previous: Algebraic Structure of the

The Gluing Condition and Topology of the Acceptance Domain

That too-short distances along 3- and 5-fold directions can be pairwise-eliminated in the tile-based construction of these tilings (and in the vertex-based construction where the too-close separations are pruned after each step) implies that the acceptance domains for the tilings glue along these directions. Since little has been said about the ADs so far except that unconstrained application of the $ \cal {G}$ operator leads to a fractal acceptance domain, it is important to consider the ADs of the tilings now. It is known that the density is invariant for each tiling constructed by inflation rules, so the implication is that each AD has the same volume.

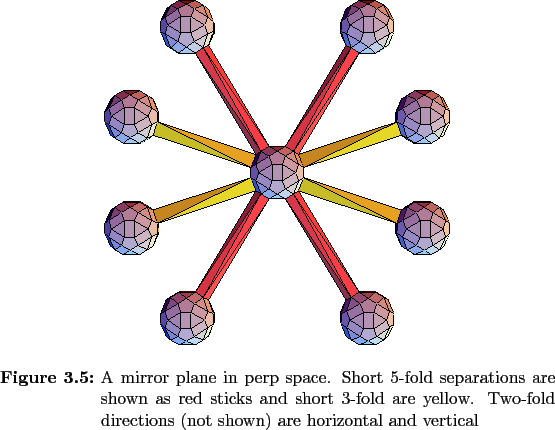
The most efficient way to look at these ADs and gain some inkling of how they are structured is to consider mirror planes normal to two-fold axes in perp space. These are the same planes used to investigate the faceting of the critical surface in Chapter 2, and they contain two-fold axes along the vertical and horizontal directions with 5-fold and 3-fold axes as shown in Figure  3.11 . Tilings whose ADs glue along both 3-fold and 5-fold directions have not been studied very much, and their only mention in the literature has been by Katz and Gratias in Reference[ 47 ], but they give no example of such an AD.

\begin{figure} % latex2html id marker 2145\epsfysize =3.in \begin{center} ... ...own) are horizontal and vertical} \normalspacing \end{center} \end{figure}

Adjusting the density in Equation  3.17 to the form dictated by the gluing condition in Equation  3.6 , reveals that these tilings do not obey the gluing condition. The SCI and BCI tilings have N 1 and N 2 equal to $ {\frac{{17}}{{10}}}$ and $ {\frac{{9}}{{10}}}$ while the FCI tilings have N 1 and N 2 valued at $ {\frac{{17}}{{40}}}$ and $ {\frac{{9}}{{40}}}$ , respectively.

To put this on a better footing, it is useful to see the form of some ADs for specific tilings. For simplicity, only ADs corresponding to BCI tilings will be discussed since these tilings have only 1 kind of AD, and the ADs for the BCI tilings illustrate the behavior of the ADs of the SCI and FCI tilings. The differences in the ADs formed by all the inflation rules (whether BCI, FCI, or SCI) is evident in the regions of perp space corresponding to the too-short separations of the un-pruned vertex set $ \cal {S}$ of Equation  3.10 . For the BCI case, there is a single way along a 3-fold direction and a single way along a 5-fold direction that two ADs related by a too-short separation along the symmetry direction (3- or 5-fold) in perp space glue together. For the SCI and FCI tilings, there is in general more than one way two ADs will glue along these too-short separations. For the SCI tilings, the ADs decorating integral lattice points will glue along 3-fold directions to ADs decorating other integral lattice points, but the 5-fold gluing will be with ADs at half-integral lattice points. The ADs at integral and half-integral points for the SCI tilings are differentiated by gluing along the 5-fold directions but unconstrained along the 3-fold directions. For the FCI case, all 4 distinct ADs are constrained. For the BCI tilings, there is only one way the ADs glue along each too-short separation.

Figure  3.12 shows an approximation to the AD formed by defining $ \cal {P}$ to always select the member of the too-close pair that is in perp space closest to x 0 . A slice of this AD in a mirror plane is shown in Figure  3.13 . A mirror-plane view of the AD that results when the furthest point from x 0 is chosen yields the AD shown in Figure  3.14 . This AD is clearly a fractal object, displaying some features of self-similarity.

\begin{figure} % latex2html id marker 2168 \begin{center} \leavevmode\epsf... ...t of the fitting to a polyhedron.} \normalspacing \end{center} \end{figure}

\begin{figure} % latex2html id marker 2175 \begin{center} \leavevmode\epsf... ...inflation rules of this Chapter.} \normalspacing \end{center} \end{figure}

\begin{figure} % latex2html id marker 2182 \begin{center} \leavevmode\epsf... ...he red along a 5-fold direction.} \normalspacing \end{center} \end{figure}

It is apparent from these figures that portions of the boundaries glue along both 5- and 3-fold directions and that the gluing is not one-to-one. Parts of the 3-fold gluing boundary also overlap with those of other 3-fold directions, or with the 5-fold direction.

next up previous
Next: Core and Variable Vertices Up: An Ensemble of Quasiperiodic Previous: Algebraic Structure of the
Chris Kimmer 2011-06-01

cjkimmer -at- ius.edu